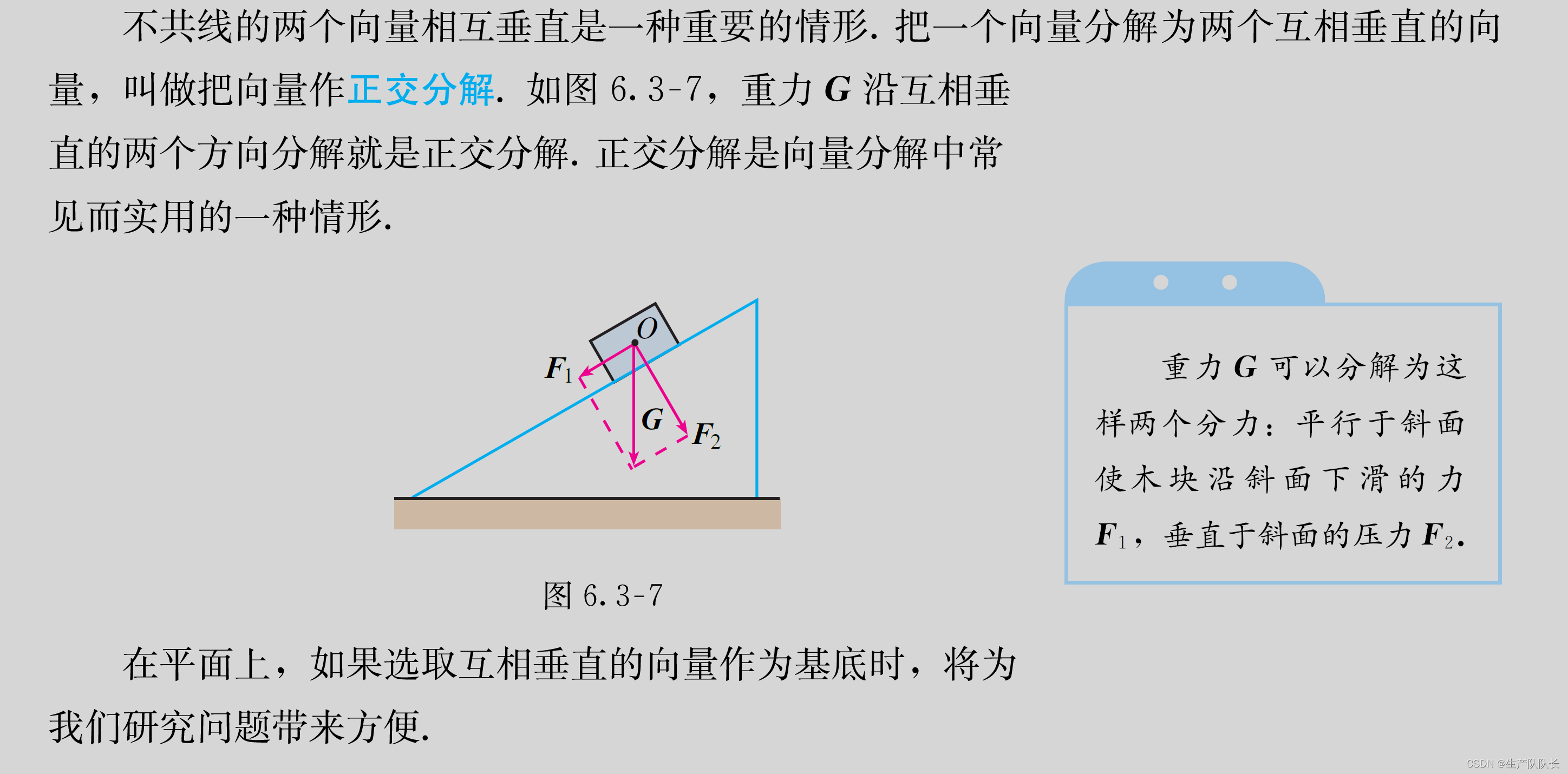
一、正交分解
二、坐标表示

这里注意一点
坐标A(x,y)与向量
a
→
\mathop{a}\limits ^{\rightarrow}
a→的坐标记作:
a
→
\mathop{a}\limits ^{\rightarrow}
a→=(x,y),表示方式的区别
引申


三、加减运算的坐标表示

四、数乘运算的坐标表示

引申
两向量共线,则对应坐标交叉相乘的差是0

五、数量积的坐标表示

六、练习
例题1
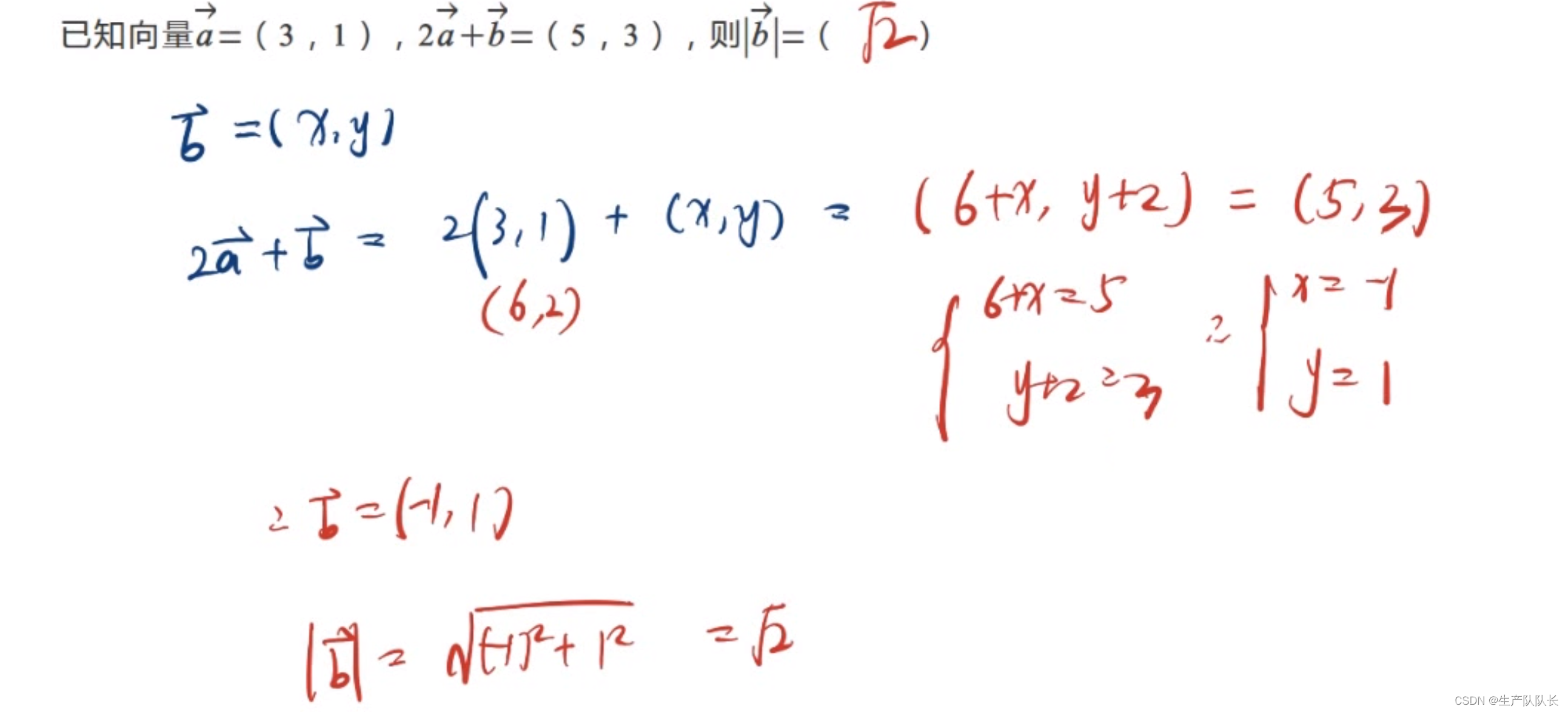
例题2
两向量共线,则对应坐标交叉相乘的差是0
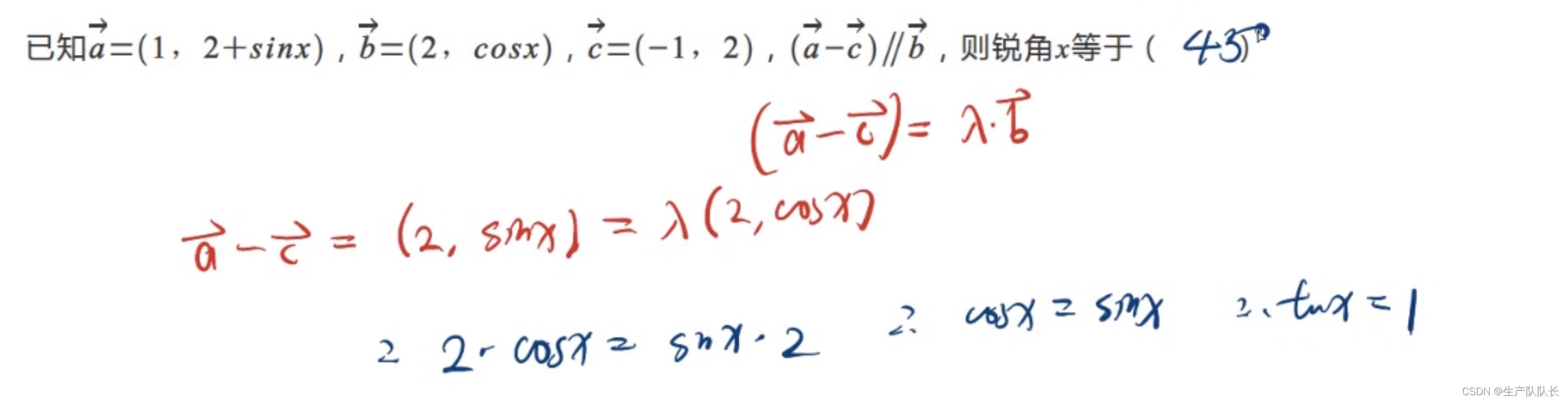
例题3
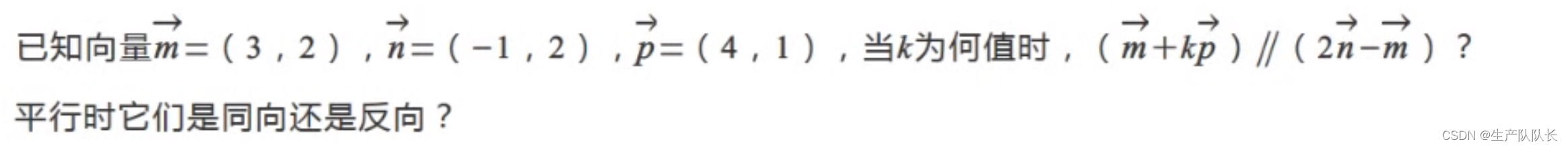
解析
这一题的第二小问,同向还是反向,要看
a
→
\mathop{a}\limits ^{\rightarrow}
a→ = λ
b
→
\mathop{b}\limits ^{\rightarrow}
b→,这里的λ与0的大小关系。大于0,同向,小于0反向。
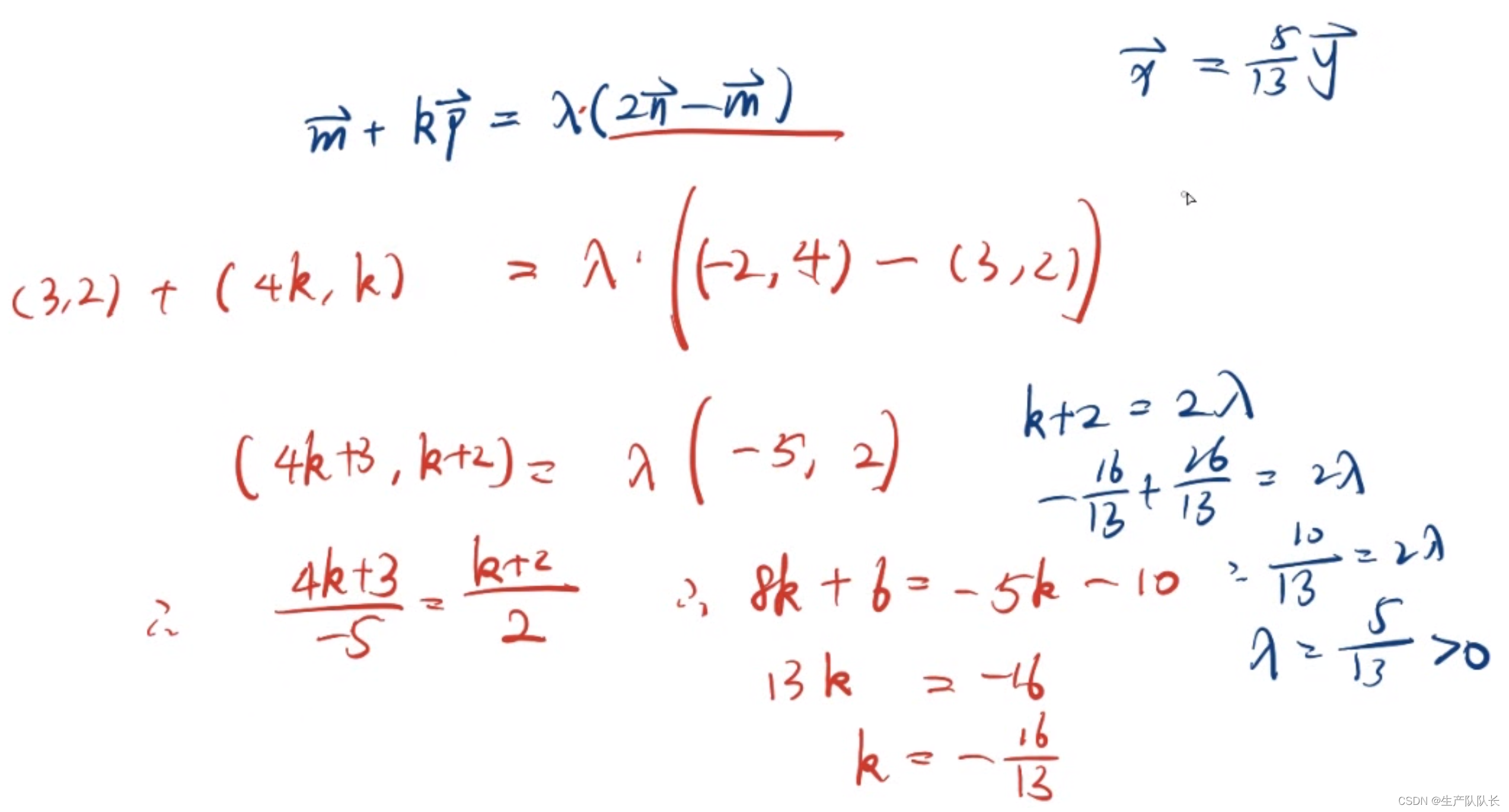
例题4

解析:
因为P在AM和BN上,于是,可以列出两个方程,从而求出P点坐标。
至于,λ的值,取其中的横坐标或者纵坐标进行列式求解即可。
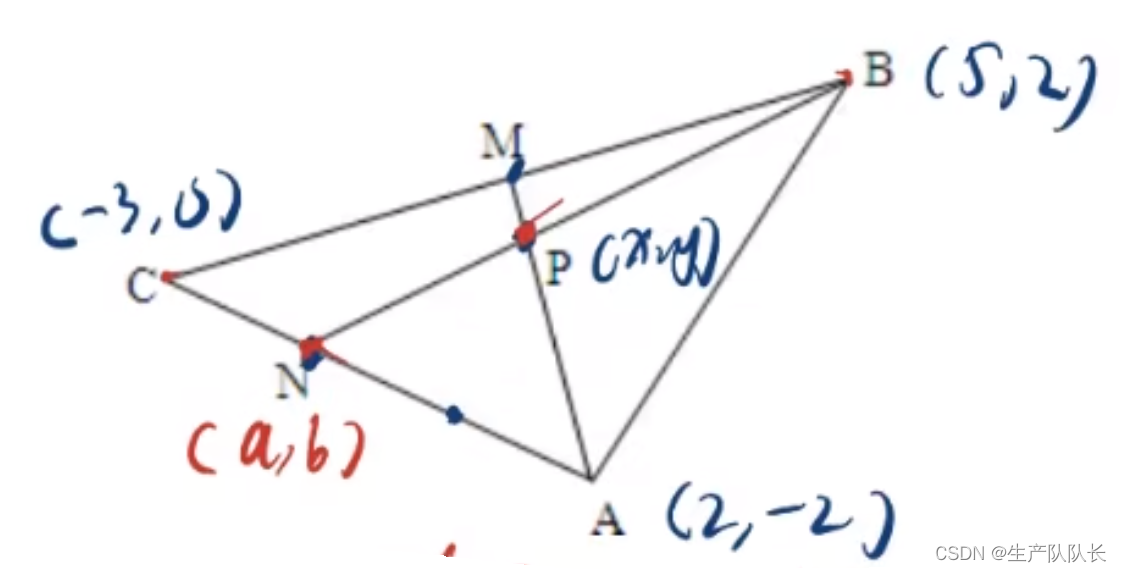
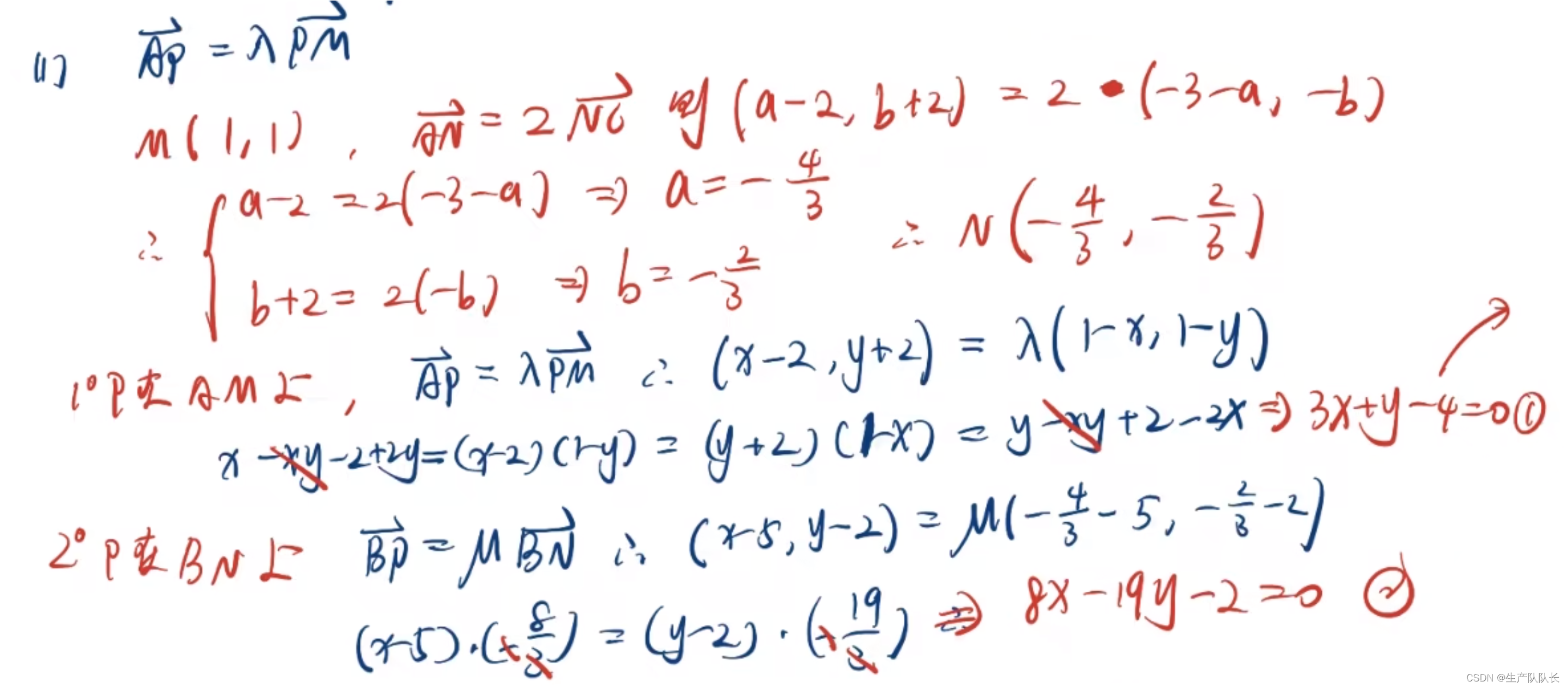
该题,还可以用初中知识解答,列直线方程,找出直线BN和AM的交点P,从而得解。