文章目录
1. 前言
1.1 贪心算法介绍
贪心算法(Greedy Algorithm)是一种在每一步选择中都采取当前状态下最优决策的算法。贪心算法通常用来解决最优化问题,其核心思想是通过局部最优解逐步推导出全局最优解。
在贪心算法中,我们并不总是考虑到未来可能发生的情况,而是只关注当前的最优选择。这种贪心选择性质使得贪心算法特别适合解决那些具有最优子结构性质的问题,即局部最优解能够推导出全局最优解的问题。
贪心算法的基本思路可以总结为以下几步:
- 确定问题的最优子结构:问题的最优解可以通过子问题的最优解逐步推导得到。
- 构造贪心选择:在每一步都做出当前状态下的最优选择,即局部最优解。
- 证明贪心选择性质:证明每一步的贪心选择都是最优的,能够推导出全局最优解。
需要注意的是,贪心算法并不适用于所有的问题,因为并非所有问题都具有最优子结构性质。在某些情况下,贪心算法得到的结果可能并不是全局最优解,而只是一个较好的解。因此,在应用贪心算法时,需要仔细分析问题的特性,以确定贪心算法是否适用于该问题。
下面我们会解决一些 数组相关的算法题(子数组、子序列类问题)
2. 算法题
2.1_将数组和减半的最少操作次数

- 题意分析:题目要求将数组nums的数组和至少减少一半的最少操作数
-
思路分析:要求使数组和减少一半的最少操作,自然我们可以每次对最大的数进行减半操作(贪心),如何进行?—— 利用堆
- 此时就有了思路:将数组元素加入到堆heap中,统计数组和的一半sum后,通过一个循环每次提取堆顶元素进行减半,直到sum<=0
代码:
class Solution {
public:
int halveArray(vector<int>& nums) {
priority_queue<double> heap;
// 统计sum
double sum = 0.0;
for(auto x : nums)
{
heap.push(x);
sum += x;
}
sum /= 2.0;
// 统计最少操作次数
int count = 0;
while(sum > 0)
{
double tmp = heap.top() / 2;
heap.pop();
sum -= tmp;
++count;
heap.push(tmp);
}
return count;
}
};
2.2_最大数

- 题意分析:题目要求将给定的一组整数重排使其最大
-
思路分析:要得到最大的重排结果,自然会想到将更大的数放到前面(贪心),这里如何排列顺序就是重点
-
思路:
- 将所给的数转为字符串,便于设定规则比较
- 由于字符串是根据字典序比较的,“23” > “221”,排到前面,是和我们想要的规则一致的,则直接对字符串数组进行排序(根据两个元素的先后顺序大小)
- 最后提取结果即可(注意全0的情况)
-
思路:
代码:
class Solution {
public:
string largestNumber(vector<int>& nums) {
// 将数字转换为字符串
vector<string> strs;
for(auto x : nums) strs.push_back(to_string(x));
// 根据字符串排序
// s1s2 > s2s1 则 s1s2在前,s2s1在后
sort(strs.begin(), strs.end(), [&](const string& s1, const string& s2){
return s1 + s2 > s2 + s1;
});
// 提取结果
string ret;
for(auto s : strs)
ret += s;
// 判断特殊情况:000000...->0
if(ret[0] == '0') return "0";
return ret;
}
};
2.3_最长递增子序列

- 题意分析:题目要找到数组的最长递增子序列的长度
-
思路分析:首先对于这道题,是可以利用动态规划解题的;而对于贪心,我们可以用一个数组存放长度为n时的最后一位元素是什么,具体规则在下图:
-
思路:

- 找ret中大于nums[i]的最小值的过程可以用二分查找进行优化
-
思路:
代码:
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
// 贪心
vector<int> ret;
ret.push_back(nums[0]);
for(int i = 0; i < nums.size(); ++i)
{
if(nums[i] > ret.back()) {
ret.push_back(nums[i]);
} else { // 二分查找
int left = 0, right = ret.size() - 1;
while(left < right)
{
int mid = (left + right) >> 1;
if(ret[mid] < nums[i])
left = mid + 1;
else
right = mid;
}
ret[left] = nums[i]; // 插入
}
}
return ret.size();
}
};
2.4_递增的三元子序列
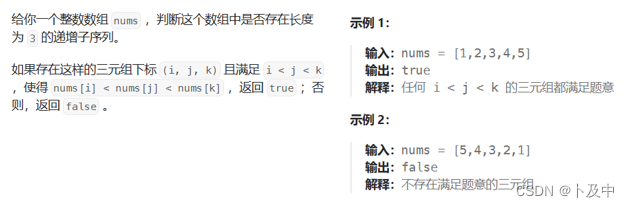
- 题意分析:题目要求找是否存在长度为3的递增子序列,实际上算是前面递增子序列的变体。
-
思路分析:同理于上一题,首先可以使用动态规划解决,每次计算判断是否dp[i]为3即可,对于贪心,我们依然采取一样的策略,但可以进行优化
- 思路:
- 用变量a表示长度为1时的元素,变量b表示长度为2 的最后一位元素,遍历数组,只要存在一个nums[i] > b,就证明有长度为3的递增子序列
代码:
class Solution {
public:
bool increasingTriplet(vector<int>& nums) {
int a = nums[0], b = INT_MAX;
for(auto x : nums)
{
if(x > b) return true;
else if (x > a) b = x;
else a = x;
}
return false;
}
};
2.5_最长连续递增序列

- 题意分析:读题后发现,该题实际上就是找最长的递增子数组(子数组和子序列的区别就在于是否连续)
-
思路分析:对于连续子数组,可以直接利用双指针进行解题:
- 思路:
- 创建两指针left、right
- 遍历数组,如果出现递增则right++,否则就更新结果并将left移动到right位置,继续寻找;
代码:
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
vector<int> tmp(nums.begin(), nums.end());
tmp.push_back(INT_MIN); // 用于简化特殊处理
int ret = 0;
int i = 0, j = 1; // 即left 于 right
while (i < tmp.size() && j < tmp.size()) {
if (tmp[j - 1] < tmp[j]) {
++j;
} else {
// 更新结果 + 移动 i 指针
ret = max(ret, j - i);
i = j; // 将 i 指针移到 j 的位置继续寻找连续递增子序列
++j; // 同时移动 j 指针
}
}
return ret;
}
};
2.6_数组中的最长连续子序列
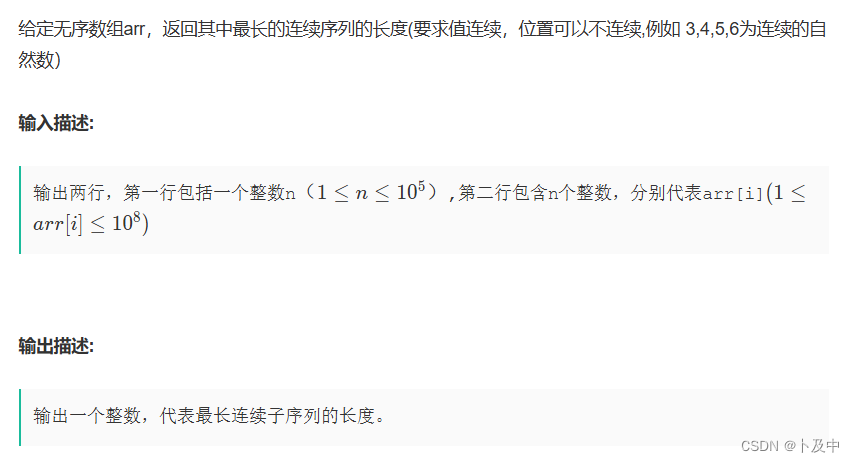

- 题意分析:题目要求找到连续子序列,注意这里的连续要求的是值连续,位置不用连续(所以可以先进行排序、排序后本质就变成了子数组问题)
-
思路分析:这道题可以使用哈希表;这里我们先排序、随后遍历数组,利用两个变量(curLen、maxLen)解题。
- 思路:
- 创建变量curLen(当前连续子序列的长度)、maxLen(连续子序列的最大长度)
- 遍历数组,i指针用于遍历数组,当出现连续,则cur++,不连续就更新结果值max,并重置cur
- (本质是和双指针一样的

)
代码:
int MLS(vector<int>& arr) {
sort(arr.begin(), arr.end());
int curLen = 1, maxLen = 1;
for (int i = 1; i < arr.size(); ++i)
{
if (arr[i - 1] != arr[i]) // 不等于前一元素
{
if (arr[i - 1] + 1 == arr[i]) { // 连续
curLen++;
}
else { // 不连续
maxLen = max(maxLen, curLen);
curLen = 1;
}
}
}
return max(curLen, maxLen);
}
2.7_在字符串中找出连续最长的数字串

- 题意分析:题目要求找到字符串中的最长连续数字串,即最长的数字子数组
-
思路分析:自然我们可以使用双指针来解题:
- 思路:
- i指针负责遍历数组,一直++,直到遇到数字串时,将j数组移动到i的位置用来遍历该数字串,走出数字串后更新结果
- 需要注意的是该题会存在多个长度一样的数字串,所以需要用一个string数组来存储结果。
代码:
int findLongestNumSub() {
string s;
while (cin >> s) {
int maxLen = 0; // 最长数字串的长度
vector<string> substrings; // 存储最长数字串
int i = 0, j = 0;
while (i < s.size()) {
while (i < s.size() && !(s[i] >= '0' && s[i] <= '9')) {
++i;
}
j = i;
while (j < s.size() && s[j] >= '0' && s[j] <= '9') {
++j;
}
if (j - i > maxLen) {
maxLen = j - i;
substrings.clear();
substrings.push_back(s.substr(i, maxLen));
}
else if (j - i == maxLen) {
substrings.push_back(s.substr(i, maxLen));
}
i = j; // 移出数字串
}
for (const auto& sub : substrings) {
cout << sub;
}
cout << "," << maxLen;
cout << endl;
} // end while
return 0;
}