文章目录
0 简介
🔥 优质竞赛项目系列,今天要分享的是
基于机器视觉的试卷系统 - opencv python 视觉识别
该项目较为新颖,适合作为竞赛课题方向,学长非常推荐!
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate
1 项目背景
机器视觉的发展对存在的作业批改问题, 提供了有效的解决方案。 通过基于机器视觉的作业批改系统可以对老师的教学工作进行辅助,改变传统的批改作业方式,
帮助老师减轻教学压力和工作负担, 老师可以快速完成批改过程,及时反馈给学生。 家长同样需要从繁重的重复性检查作业工作中解脱出来,
将更多的精力放在关注学生的学习情况和发现学习问题上。 学生可以通过自我批改作业中发现问题、加深理解, 培养自主学习意识, 提高分析问题和解决问题的能力。
因此, 自动批改作业系统在教育领域的应用表现出了无可比拟的教育价值和发展前景。


2 项目目的
在教育领域中人工智能应用愈加广泛, 作业在教学过程中起到重要的作用,当前作业批改存在着重复劳动、 效率低下等诸多问题,
这种传统的批改作业方式占据了老师宝贵的时间。 本文设计一种作业批改视觉系统, 将人工智能应用到教育领域中, 改变老师传统的批改作业方式,
实现自动批改数学算式作业的任务。
学长设计了一个系统系统,可以协助老师和家长完成繁重和重复的作业批改和检查工作, 提高工作效率。
3 系统设计
3.1 目标对象
学长这里以数学作业试卷识别为目标。

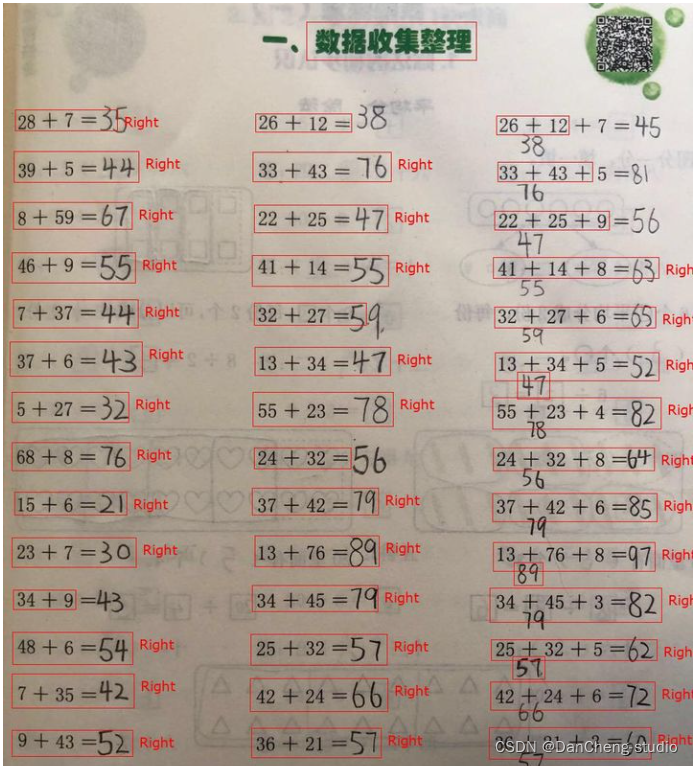
数学作业图像中一列包含多个算式, 字符主要包括印刷体的算式题目和手写体答案组成, 如上图 所示为一张数学算式作业图像。
本课题的难点在于如何有效的去除光线等外部干扰因素, 准确的提取到作业图像中的单个算式信息;选取有效的字符识别算法,
针对印刷体字符和手写体字符设计混合字符分类器,进行有效、 快速的识别; 选取适合的嵌入式设备, 进行软件与硬件的系统集成,实现视觉系统的基本功能,
完成稳定性的批改过程。
3.2 系统架构
通过对视觉系统的研究以及完成作业批改解决方案的设计目标, 采取 PC 平台与嵌入式平台相结合的设计方案。 针对 PC 平台进行软件设计与算法优化,
完成系统的功能要求后, 将程序移植到嵌入式系统中, 在嵌入式设备实现系统的便捷化应用。 对于设计的系统采取多平台测试分析, 保证系统在 PC
平台准确高效的运行, 同时保证嵌入式系统中表现出稳定的性能。 系统的总体结构框图如下。
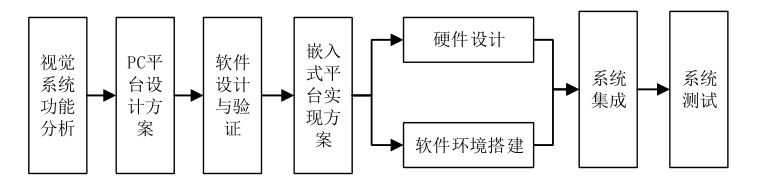
首先按照系统功能需求进行分析, 确定要完成的设计任务和目标, 并对系统的功能和性能分析做出设计要求。 其次根据系统的功能划分, 选取基于 PC
平台的软件设计方案完成软件编程, 对系统实现的功能进行验证, 测试其功能和性能是否符合设计要求。 选取视觉系统的嵌入式开发平台,
进行硬件模块设计和开发环境及软件平台的搭建, 将系统软硬件集成在一起进行调试进行, 对系统存在的问题做出改进和优化。
最后通过系统测试, 分别对系统的功能和性能进行测试验证, 是否满足设计的要求。 最终构建一款多平台应用, 基于机器视觉的自动作业批改视觉系统。
3.3 软件设计方案
该系统基于机器视觉的图像处理和字符识别技术, 整个系统的核心是软件设计部分。 能否对作业有效和快速的批改,
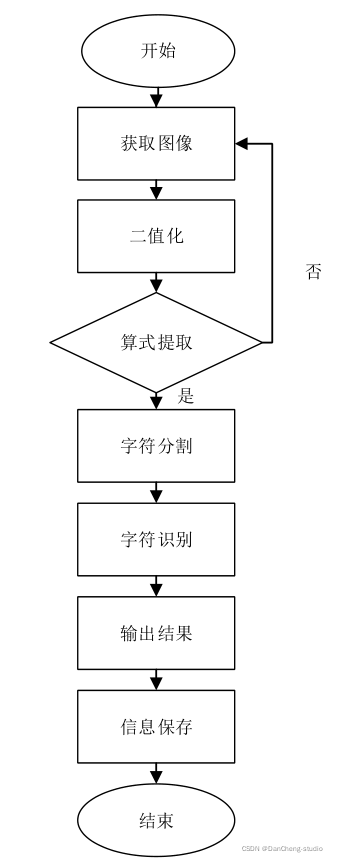
很大程度上取决于软件设计部分图像处理的效果和字符识别的准确率。 软件设计主要完成系统相关的功能操作,设计流程可分为图 中的模块组成。
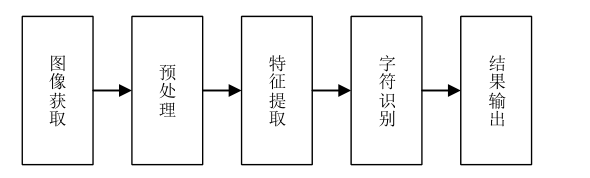
图像获取是将摄像头等设备获取的作业图像信息转化为数字图像信息; 预处理是对图像进行二值化转换, 去除多余噪声, 进行每一组算式提取,
分割获得单个清晰字符轮廓的过程; 特征提取是对预处理后的字符图像, 进行字符特征提取, 将提取好的特征量输入到分类器, 为字符识别做准备;
字符识别是系统的核心, 对字符分类器进行设计, 通过分析训练样本的特征, 将待预测的样本进行分类, 对字符完成准确识别;
结果输出是通过公式计算器计算印刷体算式结果与手写结果进行对比, 判断算式作业是否作答正确完成反馈的程。
4 图像预处理
试卷字符识别过程中, 通过摄像头采集到的纸张作业图像信息由于受到光线产生的噪声、 书写的污点等干扰因素, 影响字符图像的提取效果。
为了得到完整的字符区域特征, 同时去除无关信息的干扰, 需要对图像进行预处理操作。
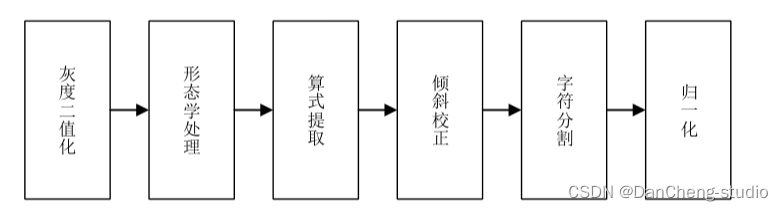
4.1 灰度二值化
灰度二值化是将图像先进行灰度处理, 再进行二值化处理。 经过灰度二值化处理的图像降低了像素的运算量, 同时突出图像中算式的特征。
灰度化是将采取到的彩色图像进行灰度值转换, 灰度化后的图像去除了彩色信息, 只保留了算式字符与背景之间的亮度信息, 图像中每个像素点都是介于 0 至 255
灰度值中的一种。

关键代码
#3、将 RGB 转为灰度图
def rgb2gray(rgb):
return np.dot(rgb[…,:3], [0.299, 0.587, 0.114])
gray = rgb2gray(lena)
# 也可以用 plt.imshow(gray, cmap = plt.get_cmap('gray'))
plt.imshow(gray, cmap='Greys_r')
plt.axis('off')
plt.show()
from scipy import misc
lena_new_sz = misc.imresize(lena, 0.5) # 第二个参数如果是整数,则为百分比,如果是tuple,则为输出图像的尺寸
plt.imshow(lena_new_sz)
plt.axis('off')
plt.show()
附上imresize的用法
功能:改变图像的大小。
用法:
B = imresize(A,m)
B = imresize(A,m,method)
B = imresize(A,[mrows ncols],method)
B = imresize(...,method,n)
B = imresize(...,method,h)
imrersize函数使用由参数method指定的插值运算来改变图像的大小。
method的几种可选值:
'nearest'(默认值)最近邻插值
'bilinear'双线性插值
'bicubic'双三次插值
B = imresize(A,m)表示把图像A放大m倍
B = imresize(...,method,h)中的h可以是任意一个FIR滤波器(h通常由函数ftrans2、fwind1、fwind2、或fsamp2等生成的二维FIR滤波器)。
4.2 形态学处理
形态学处理是通过一定形态的结构元素, 对图像产生基于形状的操作 。它可以在保持图像基本形状的基础上简化数据, 去除多余结构。
形态学运算主要包括开运算和闭运算, 这两个操作包含了膨胀和腐蚀。
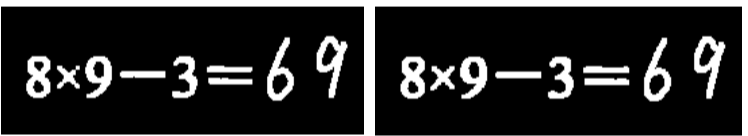
算式图像经过形态学处理后, 实验效果如上图所示。 在图中可以看出左侧的算式图像经过形态学处理之后, 其断裂的乘号字符在右侧的算式图像中形成了连通区域。
形态处理后字符整体趋于完整, 边界变的平滑。
在手写字符识别的过程中, 由于手写字符的字迹大小、 粗细程度存在的随意性很大, 在特征提取的过程中, 相同字符的冗余度导致特征向量差异很大 。
因此对获取字符图像要进行适当的细化处理, 有利于特征提取的准确性。 图像细化指将二值图像进行骨架化操作的运算, 细化操作过程就是剥离字符图像上边缘轮廓的点,
细化操作要求字符骨架保持原有的笔画特征, 不能造成笔划断开, 同时具有连续性, 字符图像应尽量保留原始的结构特征。

关键代码
import cv2 as cv
img = cv.imread(r"C:\Users\Administrator\Desktop\chinese.png")
img_cvt = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
ret,img_thr = cv.threshold(img_cvt,100,255,cv.THRESH_BINARY)
kernel = cv.getStructuringElement(cv.MORPH_RECT,(30,1)) #由于是1*30的矩阵,字体会被横向空隙的白色腐蚀掉,而下划线横向都是黑色,不会腐蚀
dst = cv.dilate(img_thr,kernel,iterations=1) #由于是白底黑字,所有进行膨胀操作来去除黑色字体
cv.imshow("img_thr",img_thr)
cv.imshow("dst",dst)
cv.waitKey(0)
cv.destroyAllWindows()
4.3 算式提取
算式提取的主要任务是从纸张中找到其中一组算式的字符区域, 并将算式从所在的区域中提取出来。 经过算式提取操作,
可以针对每一组算式进行批改,同时也便于下一步的字符分割, 算式提取准确性对作业批改效果有直接的影响。二值化处理后的算式图像中算式的灰度值为 255,
背景的灰度值为 0。
采取基于投影的方法, 进行水平和垂直方向的投影对算式进行提取 , 由于字符图像和背景图像对比度较大, 背景几乎不存在噪音干扰,
因此投影分割可以取得较好的效果。
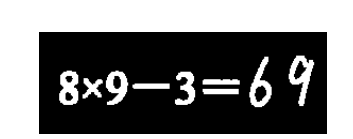
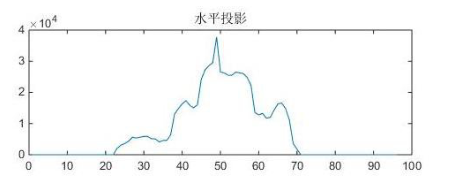
对图像进行列扫描, 得到垂直方向投影图, 投影后字符间隔的白色像素点的个数为 0, 在字符区域处形成波峰。 此时根据多个连续的波峰图像,
记录开始和结束的位置, 就可求得算式的左右边界, 进行分割得到仅包含一组算式区域的图像。
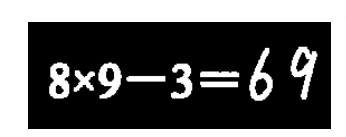
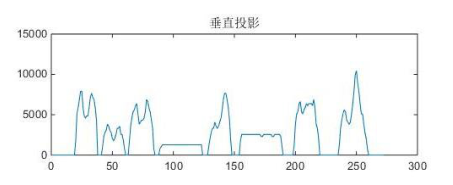
4.4 倾斜校正
在图像获取的过程中, 由于摄像头拍摄角度和作业图像有时会产生一个倾斜角度, 此时图像会发生垂直倾斜, 如果不对算式图像进行倾斜校正处理,
可能会无法正确识别出字符。 因此算式提取后要对算式图像进行倾斜校正, 采用基于 Hough 变换的方法,
其原理为图像中的直线和曲线经过变换映射到参数空间上的一个点, 通过累加的峰值检验图像中的直线和曲线。 Hough
变换的实质是将图像中一定形状元素的点进行聚类, 通过解析式将参数空间对应的点联系起来。
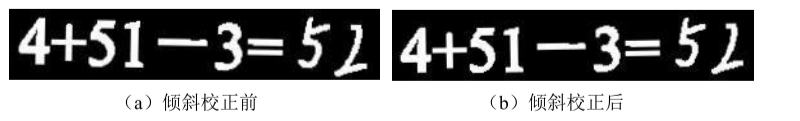
4.5 字符分割
字符分割指是将一组算式中的多个字符图像根据字符之间的空隙, 分割成多张只包含单个字符的图像,
字符分割需要保证对每个字符进行完整的提取。作业字符图像是一连串的数字算式字符, 由于算式中包含除号和等号不连通的字符图像,
因此不便采取投影法对字符进行分割。

5 字符识别
支持向量机是一种新的解决分类问题的机器学习方法, 基于统计学习理论,采用结构风险最小原则。 其原理是在训练样本集通过少量支持向量,
自动构造分类函数建立一个最大间隔分类平面, 以此解决分类问题。 支持向量机不需要构建网络结构设计, 通过非线性变换解决高维空间中样本识别问题。
支持向量机越来越多的应用到了字符识别中, 表现出较好的字符识别效果。
5.1 支持向量机原理
支持向量机(Support Vector Machine, SVM), 是 Vapnik [35] 研究小组在统计学习理论基础上, 于 1995
年针对分类问题提出的最佳分类准则。 SVM 是一种基于统计学习理论的模式识别方法, 主要应用于解决分类和回归问题。
传统的统计学理论基于样本无穷大的统计性质, SVM 专门针对有限样本, 算法转化成一个二次型寻优问题, 得到的是全局最优解。 它具有解的唯一性,
经过非线性变化转化到高维特征空间, 其算法与样本的复杂度无关, 不依赖输入空间的维数,得到的最优解优于传统的学习方法 。 因此迅速的发展起来,
在手写字符识别领域取得了巨大的成功。
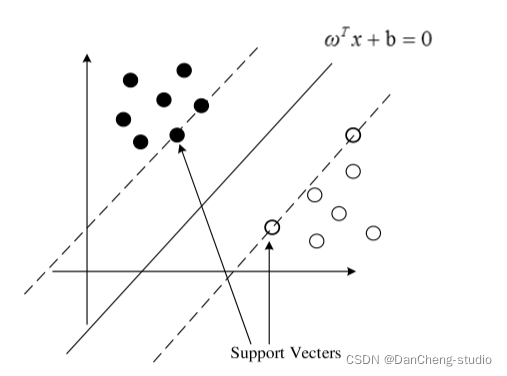
对于最优间隔平面分类问题, 根据样本分布的情况分为线性可分与非线性可分进行讨论。 在线性可分的情况下, 其目标就是寻找最优间隔超平面, 将样本准确的分开。
根据少量支持向量确定平面, 保证样本数据与超平面距离最大,如图所示。
最优分类面示意图
5.2 基于SVM的字符识别
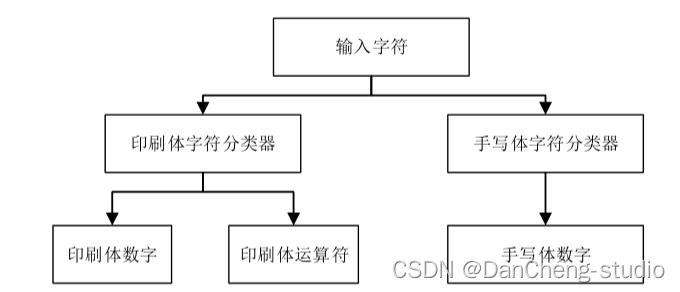
数学算式作业中包含印刷体字符和手写体字符, 将这些字符全部放在一个分类器中会导致分类过于复杂, 类别过多会使识别速率降低。
因此按照字符的分布位置将分类器分为两种类型: 印刷体字符分类器和手写字符分类器。 采取一对一分类的方法对印刷体字符和手写体字符分别设计了二分类器,
对于算式中同时包含印刷体和手写体数字字符, 选用相应的分类器, 会提高识别的准确性和速率。 如图所示, 根据字符在算式中的位置, 选用对应的分类器。
每个分类器只能将一个字符与其他字符分开, 对于手写字符而言, 其中一类字符样本的特征向量作为正集(标签对应的值为+1), 其余 9
个样本的特征向量做负集(标签对应的值为-1)。 按照这种形式依次划分, 将训练集依次进行训练, 可得到 10 个二分类器, 测试阶段将未知样本输入到这 10
个分类器进行分类判断, 决策结果取相应结果的最大值。 若输出的值为+1, 则对应相应类的字符。
网格特征是字符识别中常用的特征提取方法之一, 体现了字符形状的整体分布。 其中粗网格特征提取的方法是将字符图像等分成多个网格区域, 进行特征提取。
首先将归一化的字符样本图像, 其中大小为 128 128, 等分成 16 16 个网格, 如下图所示。
统计每个网格中黑色像素点占整个网格图像的有效像素比例, 最后将特征值按照网格排列转换为向量形式。
5.3 SVM算法实现
import numpy as np
import random
import matplotlib.pyplot as plt
'''
类名称:dataStruct
功能:用于存储一些需要保存或者初始化的数据
'''
class dataStruct:
def __init__(self,dataMatIn,labelMatIn,C,toler,eps):
self.dataMat = dataMatIn #样本数据
self.labelMat = labelMatIn #样本标签
self.C = C #参数C
self.toler = toler #容错率
self.eps = eps #乘子更新最小比率
self.m = np.shape(dataMatIn)[0] #样本数
self.alphas = np.mat(np.zeros((self.m,1))) #拉格朗日乘子alphas,shape(m,1),初始化全为0
self.b = 0 #参数b,初始化为0
self.eCache = np.mat(np.zeros((self.m,2))) #误差缓存,
'''
函数名称:loadData
函数功能:读取文本文件中的数据,以样本数据和标签的形式返回
输入参数:filename 文本文件名
返回参数:dataMat 样本数据
labelMat 样本标签
'''
def loadData(filename):
dataMat = [];labelMat = []
fr = open(filename)
for line in fr.readlines(): #逐行读取
lineArr = line.strip().split('\t') #滤除行首行尾空格,以\t作为分隔符,对这行进行分解
num = np.shape(lineArr)[0]
dataMat.append(list(map(float,lineArr[0:num-1])))#这一行的除最后一个被添加为数据
labelMat.append(float(lineArr[num-1]))#这一行的最后一个数据被添加为标签
dataMat = np.mat(dataMat)
labelMat = np.mat(labelMat).T
return dataMat,labelMat
'''
函数名称:takeStep
函数功能:给定alpha1和alpha2,执行alpha1和alpha2的更新,执行b的更新
输入参数:i1 alpha1的标号
i2 alpha2的标号
dataMat 样本数据
labelMat 样本标签
返回参数:如果i1==i2 or L==H or eta<=0 or alpha更新前后相差太小,返回0
正常执行,返回1
'''
def takeStep(i1,i2,dS):
#如果选择了两个相同的乘子,不满足线性等式约束条件,因此不做更新
if(i1 == i2):
print("i1 == i2")
return 0
#从数据结构中取得需要用到的数据
alpha1 = dS.alphas[i1,0]
alpha2 = dS.alphas[i2,0]
y1 = dS.labelMat[i1]
y2 = dS.labelMat[i2]
#如果E1以前被计算过,就直接从数据结构的cache中读取它,这样节省计算量,#如果没有历史记录,就计算E1
if(dS.eCache[i1,0] == 1):
E1 = dS.eCache[i1,1]
else:
u1 = (np.multiply(dS.alphas,dS.labelMat)).T * np.dot(dS.dataMat,dS.dataMat[i1,:].T) + dS.b #计算SVM的输出值u1
E1 = float(u1 - y1) #误差E1
#dS.eCache[i1] = [1,E1] #存到cache中
#如果E2以前被计算过,就直接从数据结构的cache中读取它,这样节省计算量,#如果没有历史记录,就计算E2
if(dS.eCache[i2,0] == 1):
E2 = dS.eCache[i2,1]
else:
u2 = (np.multiply(dS.alphas,dS.labelMat)).T * np.dot(dS.dataMat,dS.dataMat[i2,:].T) + dS.b #计算SVM的输出值u2
E2 = float(u2 - y2) #误差E2
#dS.eCache[i2] = [1,E2] #存到cache中
s = y1*y2
#计算alpha2的上界H和下界L
if(s==1): #如果y1==y2
L = max(0,alpha1+alpha2-dS.C)
H = min(dS.C,alpha1+alpha2)
elif(s==-1): #如果y1!=y2
L = max(0,alpha2-alpha1)
H = min(dS.C,dS.C+alpha2-alpha1)
if(L==H):
print("L==H")
return 0
#计算学习率eta
k11 = np.dot(dS.dataMat[i1,::],dS.dataMat[i1,:].T)
k12 = np.dot(dS.dataMat[i1,::],dS.dataMat[i2,:].T)
k22 = np.dot(dS.dataMat[i2,::],dS.dataMat[i2,:].T)
eta = k11 - 2*k12 +k22
if(eta > 0):#正常情况下eta是大于0的,此时计算新的alpha2,新的alpha2标记为a2
a2 = alpha2 + y2*(E1-E2)/eta#这个公式的推导,曾经花费了我很多精力,现在写出来却是如此简洁,数学真是个好东西
#对a2进行上下界裁剪
if(a2 < L):
a2 = L
elif(a2 > H):
a2 = H
else:#非正常情况下,也有可能出现eta《=0的情况
print("eta<=0")
return 0
'''
Lobj =
Hobj =
if(Lobj < Hobj-eps):
a2 = L
elif(Lobj > Hobj+eps):
a2 = H
else:
a2 = alpha2
'''
#如果更新量太小,就不值浪费算力继续算a1和b,不值得对这三者进行更新
if(abs(a2-alpha2) < dS.eps*(a2+alpha2+dS.eps)):
print("so small update on alpha2!")
return 0
#计算新的alpha1,标记为a1
a1 = alpha1 + s*(alpha2 - a2)
#计算b1和b2,并且更新b
b1 = -E1 + y1*(alpha1 - a1)*np.dot(dS.dataMat[i1,:],dS.dataMat[i1,:].T) + y2*(alpha2 - a2)*np.dot(dS.dataMat[i1,:],dS.dataMat[i2,:].T) + dS.b
b2 = -E2 + y1*(alpha1 - a1)*np.dot(dS.dataMat[i1,:],dS.dataMat[i2,:].T) + y2*(alpha2 - a2)*np.dot(dS.dataMat[i2,:],dS.dataMat[i2,:].T) + dS.b
if(a1>0 and a1<dS.C):
dS.b = b1
elif(a2>0 and a2<dS.C):
dS.b = b2
else:
dS.b = (b1 + b2) / 2
#用a1和a2更新alpha1和alpha2
dS.alphas[i1] = a1
dS.alphas[i2] = a2
#由于本次alpha1、alpha2和b的更新,需要重新计算Ecache,注意Ecache只存储那些非零的alpha对应的误差
validAlphasList = np.nonzero(dS.alphas.A)[0] #所有的非零的alpha标号列表
dS.eCache = np.mat(np.zeros((dS.m,2)))#要把Ecache先清空
for k in validAlphasList:#遍历所有的非零alpha
uk = (np.multiply(dS.alphas,dS.labelMat).T).dot(np.dot(dS.dataMat,dS.dataMat[k,:].T)) + dS.b
yk = dS.labelMat[k,0]
Ek = float(uk-yk)
dS.eCache[k] = [1,Ek]
print ("updated")
return 1
'''
函数名称:examineExample
函数功能:给定alpha2,如果alpha2不满足KKT条件,则再找一个alpha1,对这两个乘子进行一次takeStep
输入参数:i2 alpha的标号
dataMat 样本数据
labelMat 样本标签
返回参数:如果成功对一对乘子alpha1和alpha2执行了一次takeStep,返回1;否则,返回0
'''
def examineExample(i2,dS):
#从数据结构中取得需要用到的数据
y2 = dS.labelMat[i2,0]
alpha2 = dS.alphas[i2,0]
#如果E2以前被计算过,就直接从数据结构的cache中读取它,这样节省计算量,#如果没有历史记录,就计算E2
if(dS.eCache[i2,0] == 1):
E2 = dS.eCache[i2,1]
else:
u2 = (np.multiply(dS.alphas,dS.labelMat)).T * np.dot(dS.dataMat,dS.dataMat[i2,:].T) + dS.b#计算SVM的输出值u2
E2 = float(u2 - y2)#误差E2
#dS.eCache[i2] = [1,E2]
r2 = E2*y2
#如果当前的alpha2在一定容忍误差内不满足KKT条件,则需要对其进行更新
if((r2<-dS.toler and alpha2<dS.C) or (r2>dS.toler and alpha2>0)):
'''
#随机选择的方法确定另一个乘子alpha1,多执行几次可可以收敛到很好的结果,就是效率比较低
i1 = random.randint(0, dS.m-1)
if(takeStep(i1,i2,dS)):
return 1
'''
#启发式的方法确定另一个乘子alpha1
nonZeroAlphasList = np.nonzero(dS.alphas.A)[0].tolist()#找到所有的非0的alpha
nonCAlphasList = np.nonzero((dS.alphas-dS.C).A)[0].tolist()#找到所有的非C的alpha
nonBoundAlphasList = list(set(nonZeroAlphasList)&set(nonCAlphasList))#所有非边界(既不=0,也不=C)的alpha
#如果非边界的alpha数量至少两个,则在所有的非边界alpha上找到能够使\E1-E2\最大的那个E1,对这一对乘子进行更新
if(len(nonBoundAlphasList) > 1):
maxE = 0
maxEindex = 0
for k in nonBoundAlphasList:
if(abs(dS.eCache[k,1]-E2)>maxE):
maxE = abs(dS.eCache[k,1]-E2)
maxEindex = k
i1 = maxEindex
if(takeStep(i1,i2,dS)):
return 1
#如果上面找到的那个i1没能使alpha和b得到有效更新,则从随机开始处遍历整个非边界alpha作为i1,逐个对每一对乘子尝试进行更新
randomStart = random.randint(0,len(nonBoundAlphasList)-1)
for i1 in range(randomStart,len(nonBoundAlphasList)):
if(i1 == i2):continue
if(takeStep(i1,i2,dS)):
return 1
for i1 in range(0,randomStart):
if(i1 == i2):continue
if(takeStep(i1,i2,dS)):
return 1
#如果上面的更新仍然没有return 1跳出去或者非边界alpha数量少于两个,这种情况只好从随机开始的位置开始遍历整个可能的i1,对每一对尝试更新
randomStart = random.randint(0,dS.m-1)
for i1 in range(randomStart,dS.m):
if(i1 == i2):continue
if(takeStep(i1,i2,dS)):
return 1
for i1 in range(0,randomStart):
if(i1 == i2):continue
if(takeStep(i1,i2,dS)):
return 1
'''
i1 = random.randint(0,dS.m-1)
if(takeStep(i1,i2,dS)):
return 1
'''
#如果实在还更新不了,就回去重新选择一个alpha2吧,当前的alpha2肯定是有毒
return 0
'''
函数名称:SVM_with_SMO
函数功能:用SMO写的SVM的入口函数,里面采用了第一个启发式确定alpha2,即在全局遍历和非边界遍历之间来回repeat,直到不再有任何更新
输入参数:dS dataStruct类的数据
返回参数:None
'''
def SVM_with_SMO(dS):
#初始化控制变量,确保第一次要全局遍历
numChanged = 0
examineAll = 1
#显然,如果全局遍历了一次,并且没有任何更新,此时examineAll和numChanged都会被置零,算法终止
while(numChanged > 0 or examineAll):
numChanged = 0
if(examineAll):
for i in range(dS.m):
numChanged += examineExample(i,dS)
else:
for i in range(dS.m):
if(dS.alphas[i] == 0 or dS.alphas[i] == dS.C):continue
numChanged += examineExample(i,dS)
if(examineAll == 1):
examineAll = 0
elif(numChanged == 0):
examineAll = 1
'''
函数名称:cal_W
函数功能:根据alpha和y来计算W
输入参数:dS dataStruct类的数据
返回参数:W 超平名的法向量W
'''
def cal_W(dS):
W = np.dot(dS.dataMat.T,np.multiply(dS.labelMat,dS.alphas))
return W
'''
函数名称:showClassifer
函数功能:画出原始数据点、超平面,并标出支持向量
输入参数:dS dataStruct类的数据
W 超平名的法向量W
返回参数:None
'''
def showClassifer(dS,w):
#绘制样本点
dataMat = dS.dataMat.tolist()
data_plus = [] #正样本
data_minus = [] #负样本
for i in range(len(dataMat)):
if dS.labelMat[i,0] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus) #转换为numpy矩阵
data_minus_np = np.array(data_minus) #转换为numpy矩阵
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7, c='r') #正样本散点图
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7,c='g') #负样本散点图
#绘制直线
x1 = max(dataMat)[0]
x2 = min(dataMat)[0]
a1, a2 = w
b = float(dS.b)
a1 = float(a1[0])
a2 = float(a2[0])
y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
plt.plot([x1, x2], [y1, y2])
#找出支持向量点
for i, alpha in enumerate(dS.alphas):
if abs(alpha) > 0.000000001:
x, y = dataMat[i]
plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
plt.xlabel("happy 520 day, 2018.06.13")
plt.savefig("svm.png")
plt.show()
if __name__ == '__main__':
dataMat,labelMat = loadData("testSet.txt")
dS = dataStruct(dataMat, labelMat, 0.6, 0.001, 0.01)#初始化数据结构 dataMatIn, labelMatIn,C,toler,eps
for i in range(0,1):#只需要执行一次,效果就非常不错
SVM_with_SMO(dS)
W = cal_W(dS)
showClassifer(dS,W.tolist())
6 算法测试
输入图像

预处理结果

识别结果
7 系统实现
系统主要流程如下
对在 PC 软件平台通过 MFC 界面中实现各模块操作, 系统界面如图所示。
系统界面采用模块化设计, 按照界面分布分为图像显示模块、 按键功能模块、 图像预处理模块、 批改结果输出四个模块组成。
主要内容包括:
- 显示获取作业图像的基本信息;
- 通过按键控制相应功能;
- 显示预处理后图像的效果;输出识别的字符信息和批改的结果。
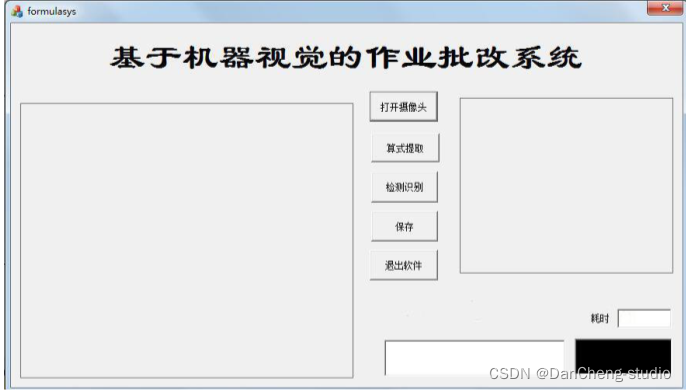
图像显示模块, 通过打开摄像头按键, 将摄像头获取到的纸张作业图像实时信息传送到计算机中, 获取的图像显示在界面左侧窗口, 界面运行结果如图所示。

按键功能模块, 通过算式提取按键, 对纸张中单个算式整体区域进行选框提取, 运行结果如图所示,
此时算式检测的结果在原图像上用矩形框标记,在界面右侧显示提取到的算式效果。

图像处理模块, 通过检测识别按键完成字符分割和识别, 在界面右侧窗口显示预处理后的图像效果。 批改结果输出模块,
在界面下框中显示字符的识别结果以及手写的计算结果, 同时在右下角窗口显示解答正误, 输出得到的批改信息。 同时对整个过程运行的时间进行统计,
最后保存按键将错误的批改结果保存, 便于后期修改。 此时系统运行界面如图所示。

8 最后
🧿 更多资料, 项目分享: