基于matlab的自适应阈值法图像分割

1 原理

自适应阈值法图像分割的原理是基于图像的局部统计信息来确定每个像素的阈值。这种方法通过将图像划分为多个小区域，并根据每个区域的统计结果计算出相应的阈值。这样做的好处是能够在不同的光照条件下自动调整阈值，从而更好地适应不同图像的分割需求。

本文采用的是自适应阈值法的一种常见实现方式：大津阈值法（OTSU方法），也被称为最大类间方差法。以下是该方法的基本原理和公式：

1.1 原理

图像灰度化：首先，将输入的彩色图像转换为灰度图像。
计算灰度直方图：统计灰度图像中每个灰度级出现的频率，得到灰度直方图。
确定最佳阈值：通过遍历所有可能的灰度级，计算前景和背景之间的类间方差。使类间方差最大的灰度级被选作最佳阈值。
二值化：使用最佳阈值将灰度图像转换为二值图像，即前景（目标）和背景。

1.2 公式

设图像包含(L)个灰度等级，灰度值为(i)的像素点的个数为(N_i)，像素点的总个数为：

$N = N_0 + N_1 + \ldots + N_{L-1}$

灰度值为(i)的像素点的概率为：

$P_i = \frac{N_i}{N}$

图像的灰度均值为：

$u_T = \sum_{i=0}^{L-1} iP_i$

使用阈值(T)将图像分为目标(c_0)和背景(c_1)两类，则(w_0(T))和(w_1(T))分别表示阈值为(T)时，(c_0)和(c_1)发生的概率，即：

$w_0(T) = \sum_{i=0}^{T} P_i$

$w_1(T) = 1 - w_0(T)$

(c_0)和(c_1)的均值为：

$u_0(T) = \frac{\sum_{i=0}^{T} iP_i}{w_0(T)}$
$u_1(T) = \frac{u_T - \sum_{i=0}^{T} iP_i}{w_1(T)}$

类间方差(\sigma_B^2(T))表示直方图中阈值为(T)的类间方差，定义为：

$\sigma_B^2(T) = w_0(T)[u_0(T) - u_T]^2 + w_1(T)[u_1(T) - u_T]^2$

通过遍历所有可能的灰度级，找到使 $\sigma_B^2(T)$ 最大的T，即为最佳阈值。

1.3 总结

自适应阈值法图像分割通过计算图像的局部统计信息来确定每个像素的阈值，从而能够在不同的光照条件下自动调整阈值，提高图像分割的准确性和鲁棒性。大津阈值法（OTSU方法）是自适应阈值法的一种常见实现方式，它基于最大类间方差原理来确定最佳阈值。

2 代码

%% 阈值分割法  
% 读取图像    
I = imread('test.jpg');    % 确保图片路径正确  
% 如果图像是彩色的，先转换为灰度图  
if size(I, 3) == 3  
    I = rgb2gray(I);  
end  
  
% 显示原图像    
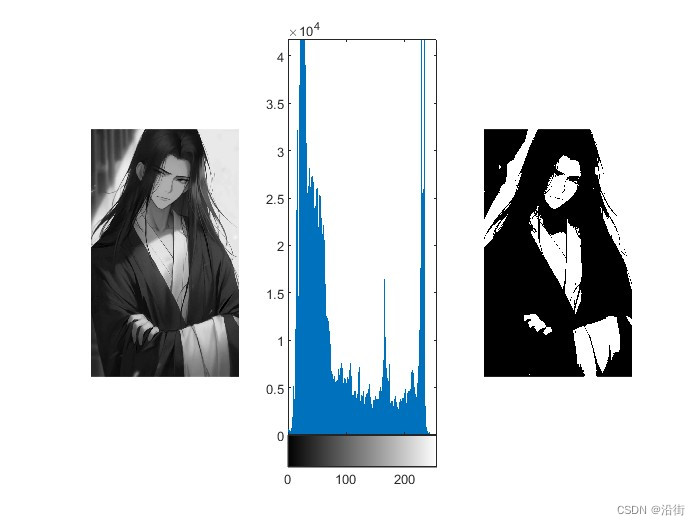
subplot(1,3,1);imshow(I);    
subplot(1,3,2);imhist(I);     
  
% 使用Otsu's方法计算阈值  
T = graythresh(I);  % 返回的T是一个0到1之间的值，表示归一化阈值  
T_scaled = round(T * 255);  % 将归一化阈值转换为0到255之间的整数阈值  
T_scaled
% 使用阈值进行图像分割  
BW = imbinarize(I, T_scaled / 255);  % 使用imbinarize函数直接进行阈值分割  
% 或者，如果您想手动实现，可以像之前那样使用循环  
% 但通常建议使用imbinarize，因为它更快且更易于阅读  
  
% 显示分割后的图像    
subplot(1,3,3);    
imshow(BW);

个人技术分享