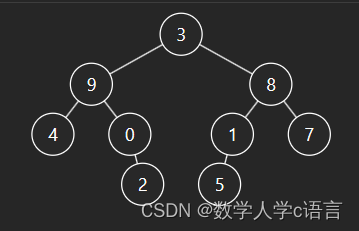
题目关键词,从左到右,从上到下,那么使用bfs宽度优先算法。
使用字典v保存每一列的值。
class Solution:
def verticalOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root: return []
v = defaultdict(list)
qu = deque()
qu.append([root, 0])
while qu:
node, column = qu.popleft()
v[column].append(node.val)
if node.left: qu.append([node.left, column - 1])
if node.right: qu.append([node.right, column + 1])
return [ v[x] for x in sorted(v.keys())]刚开始我使用的还是dfs,发现过程确实复杂一些,不能从上到下遍历。这是我原来的代码:
class Solution:
def __init__(self):
self.ans = defaultdict(dict)
self.idx = 0
def verticalOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root: return []
self.init_idx(root, 0)
self.dfs(root, -self.idx, 0)
ans = []
k1 = sorted(self.ans.keys())
for x in k1:
ans.append([])
k2 = sorted(self.ans[x].keys())
for y in k2:
ans[-1] += self.ans[x][y]
return ans
def init_idx(self, root, idx):
if root.left:
self.init_idx(root.left, idx - 1)
if root.right:
self.init_idx(root.right, idx + 1)
self.idx = min(self.idx, idx)
def dfs(self, root, idx, idy):
if not root: return
if idy not in self.ans[idx]:
self.ans[idx][idy] = [root.val]
else:
self.ans[idx][idy].append(root.val)
self.dfs(root.left, idx-1, idy + 1)
self.dfs(root.right, idx+1, idy + 1)
回顾一下,发现init_idx这个函数没必要,他目的是,如果中间节点root的列的编号为0,那么最左边节点的列的编号为self.idx,可以推出,如果最左边节点列的编号为0,那么root排在第-self.idx列。
可以省掉这一步,直接设置root节点为第0列,左节点为-1列,右节点为第1列,最后在把列排个序。这样的话,左节点-1直接变道0,root变道1,右节点变道2.