决策树学习笔记

一、衡量标准——熵

$H(X)=-\sum p_i \log(p_i)$

随机变量不确定性的度量

信息增益：表示特征X使得类Y的不确定性减少的程度。

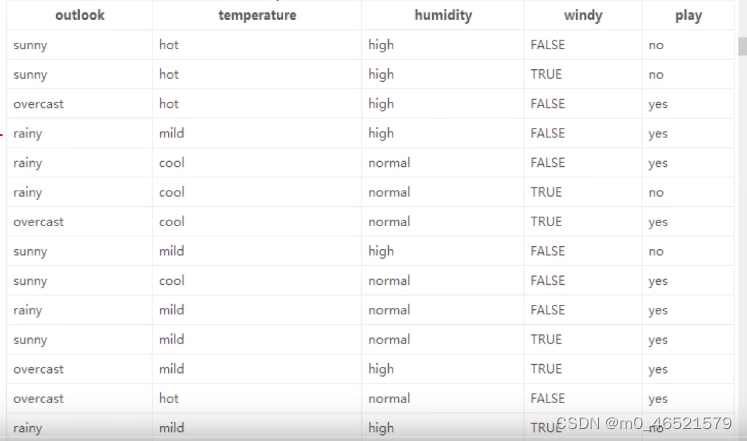
14天的打球情况

特征：4种环境变化（天气、温度等等）

在上述数据种，14天中打球的天数为9天；不打球的天数为5天，计算熵值为

$H(X)=-\frac{5}{14} \log(\frac{5}{14}) - \frac{9}{14} \log(\frac{9}{14}) = 0.940$

（1）选择outlook作为根节点

计算加权

$\frac{5}{14}*0.971+\frac{4}{14}*0+\frac{5}{14}*0.971=0.693$

gain(outlook) = 0.940-0.693 = 0.247

类似计算：

gain(temp) = 0.029

gain(humidity) = 0.152

gain(windy) = 0.048

outlook的信息增益最大，因此选择outlook作为根节点

以此类推，确定每一个子树的根节点

ID3: 信息增益

C4.5: 信息增益率

CART: GINI系数

$1-\sum p_k^2$

决策树过拟合风险很大，理论上可以将数据完全分开，即一个叶子节点一个数据，因此需要对决策数进行剪枝操作。

剪枝策略：预剪枝和后剪枝

预剪枝：边建立决策树边进行剪枝操作

后剪枝：当建立完决策树后来进行剪枝操作