文章目录
基本概念
事件
事件:某种情况的“陈述”
⇒
\Rightarrow
⇒ 事件A:掷出的骰子为偶数点
⇒
\Rightarrow
⇒ 事件A包含多种结果,每种结果都是一个基本事件
⇒
\Rightarrow
⇒ 事件的本质是集合
事件之间的基本关系:
- 蕴含与相等:如果当A发生时B必发生 ,记数学公式: A ⊂ B A \subset B A⊂B数学公式: ⇒ \Rightarrow ⇒当数学公式: A , B A,B A,B相互蕴含时,两式相等,记数学公式: A = B A=B A=B
- 互斥与对立:在一次试验中不可能同时发生,但可以都不发生,有A就没有B,有B没有A,但是可以同时没有A和B数学公式: ⇒ \Rightarrow ⇒A为一事件,则事件 B={A不发生} ,则A和B互为对立事件
- 事件和(或称并集):A和B中至少发生一个(并集),记数学公式: C = A + B C=A+B C=A+B
- 事件积(或称交集):A发生且B发生(交集),记数学公式: C = A B C=AB C=AB
- 事件差:A发生且B不发生,记数学公式: C = A − B C=A-B C=A−B
全概率公式:一个事件的概率,该事件可以表示为若干互斥事件的联合

随机变量
随机变量是实验结果的函数 ⇒ \Rightarrow ⇒抛一枚硬币,定义1=正面朝上 ,0=反面朝上,所以随机变量 X X X就代表抛硬币这个试验的结果,要么0要么1
独立同分布
独立性:一个随机变量的取值不会影响另一个随机变量的取值
同分布:所有随机变量服从相同的概率分布
离散型随机变量
伯努利分布(两点分布)
伯努利分布:两种可能结果的实验(如成功和失败),成功的概率为
p
p
p,失败的概率为
1
−
p
1-p
1−p
概率密度函数:
P
(
X
=
x
)
=
{
p
if
x
=
1
1
−
p
if
x
=
0
P(X=x)=\begin{cases}p&\text{if}\ \ x=1\\1-p&\text{if}\ \ x=0\end{cases}
P(X=x)={p1−pif x=1if x=0
期望值:
E
(
X
)
=
p
E(X)=p
E(X)=p
方差:
V
a
r
(
X
)
=
p
(
1
−
p
)
Var(X)=p(1-p)
Var(X)=p(1−p)
二项分布
二项分布:n次独立同分布的伯努利试验的成功次数的分布,每次试验成功的概率为
p
p
p 概率密度函数:
P
(
X
=
k
)
=
(
n
k
)
p
k
(
1
−
p
)
n
−
k
P(X=k)=\binom{n}kp^k(1-p)^{n-k}
P(X=k)=(kn)pk(1−p)n−k
期望值:
E
(
X
)
=
n
p
E(X)=np
E(X)=np
方差:
V
a
r
(
X
)
=
n
p
(
1
−
p
)
Var(X)=np(1-p)
Var(X)=np(1−p)
几何分布
几何分布:在第一次成功之前的失败次数(包括第一次成功),每次试验成功的概率为
p
p
p
概率密度函数:
P
(
X
=
k
)
=
(
1
−
p
)
k
p
for
k
=
0
,
1
,
2
,
…
P(X=k)=(1-p)^kp\quad\text{for}\ \ k=0,1,2,\ldots
P(X=k)=(1−p)kpfor k=0,1,2,…
期望值:
E
(
X
)
=
1
−
p
p
E(X)=\frac{1-p}p
E(X)=p1−p
方差:
Var
(
X
)
=
1
−
p
p
2
\operatorname{Var}(X)=\frac{1-p}{p^2}
Var(X)=p21−p
泊松分布
泊松分布:单位时间或空间内某事件的发生次数,在一个间隔中平均发生事件的次数由
λ
\lambda
λ决定,
λ
\lambda
λ是事件发生比率
概率密度函数:
P
(
X
=
k
)
=
λ
k
e
−
λ
k
!
P(X=k)=\frac{\lambda^ke^{-\lambda}}{k!}
P(X=k)=k!λke−λ
期望值:
E
(
X
)
=
λ
E(X)=\lambda
E(X)=λ
方差:
Var
(
X
)
=
λ
\operatorname{Var}(X)=\lambda
Var(X)=λ
“事件”可理解为一天中网站的访客数、一天中所接到的电话数
例如:每周平均有15个人给我的博客点赞,我想预测下一周的点赞数
如果使用二项分布来解决,令
x
x
x表示在
n
n
n次重复实验中发生点赞的次数,
p
p
p表示每次实验的点赞概率(Probability)。我们现在已知的是每周平均的点赞比率(rate)为15个赞/周,并不知道点赞概率
p
p
p和博客访客数
n
n
n的任何信息
假设过去的1年(=52周)的数据中,一共有
10000
10000
10000人看了我的博客,其中有
800
800
800个人点赞了,这样平均每周访客数
=
10000
/
52
=
192
=10000 / 52 = 192
=10000/52=192,平均每周点赞数
=
800
/
52
=
15
=800 / 52 = 15
=800/52=15,可得到概率
p
=
800
/
10000
=
0.08
=
8
%
p = 800 / 10000 = 0.08 = 8 \%
p=800/10000=0.08=8%
使用二项分布的概率密度函数,预测下一周有20个人点赞的概率为:
B
i
n
(
m
=
20
∣
N
=
192
,
p
=
0.08
)
=
N
!
(
N
−
m
)
!
m
!
p
m
(
1
−
p
)
N
−
m
=
0.04657
\mathrm{Bin(m=20\mid N=192,p=0.08)=\frac{N!}{(N-m)!m!}p^m(1-p)^{N-m}=0.04657}
Bin(m=20∣N=192,p=0.08)=(N−m)!m!N!pm(1−p)N−m=0.04657
在上述过程中,可以将x=该周有15次点赞,也可以是x=该天有
15
/
7
=
2.1
15/7=2.1
15/7=2.1个赞,也可以是x=该小时有
15
/
7
∗
24
=
0.1
15/7*24=0.1
15/7∗24=0.1个赞,这意味着大多数小时没有赞,而有的小时有一个点赞。仔细想想,似乎一定时间内出现超过1个点赞的情况也是合理的(比如文章早上刚发布的时候)。由此,二项分布的问题是它无法在一个时间单元中包含超过1次的事件(在这里,时间单元是1小时)
那么,我们将1小时切分成60分钟,时间单元是1分钟,使得1小时能够包含多个事件。问题得到解决了吗?还没有,比如何同学的5G视频,一晚上点赞就过百万,1分钟内不止一个赞。那我们再将时间单元切分成秒,这样1分钟又能包含多个事件。这样思考下去,我们会将已有的事件单元不断地切分,直到满足一个时间单元只包含一个事件,而大的时间单元能够包含1个以上的事件
形式化来看,这意味着
n
→
∞
n\to \infty
n→∞,当我们假定比率(rate)固定,则必须让
p
→
0
p\to 0
p→0,否则点赞数
n
×
p
→
∞
n \times p \to \infty
n×p→∞
基于以上的约束,时间单元变得无穷小。我们不用担心同一个时间单元包含一个以上的事件了
在用二项分布时,无法直接用比率(rate)来计算点赞概率
p
p
p,而是需要
n
n
n和
p
p
p才能使用二项分布的概率密度函数,而泊松分布不需要知道
n
n
n和
p
p
p,它假定
n
n
n是一个无穷大的数,而
p
p
p是无穷小的数,泊松分布唯一参数是比率
λ
\lambda
λ。现实中,得知
n
n
n和
p
p
p得进行很多次实验,而短时间内,比率(rate)很容易得到(例如,在下午2点-4点,收到了4个点赞)


泊松分布的假设:每个时间单元的事件平均发生比率是常数
例如:博客的每小时平均点赞数不太可能服从泊松分布,而博客每个月的平均点赞数可近似看作是固定的。假如你的博客写的很好,被公众号转发推广了,那可能会有大批的读者来阅读,这种情况下的点赞数就不满足泊松分布了
泊松分布的适用条件:
- 事件独立性:事件的发生是相互独立的,例如,每个读者对文章的点赞行为不受其他读者行为的影响
- 事件发生概率相等:每个事件在单位时间或空间内发生的概率是相同的
- 单位时间或空间内事件的发生率固定:单位时间或空间内事件的平均发生次数( λ \lambda λ)是固定的
当博客被公众号转发推广后,会出现以下变化:
- 读者行为不再独立:由于公众号转发,读者可能会集中在某个时间段内大量访问博客,导致点赞行为之间不再独立。例如,一个读者点赞后,可能会引起更多读者来点赞,这种情况下点赞行为具有相关性
- 事件发生概率不再相等:在被转发推广的时段,点赞的概率可能会显著提高,导致某些时间段内的点赞率远高于平时
- 事件发生率不固定:被推广后,单位时间内的访问量和点赞量会显著增加,不再符合泊松分布所要求的固定事件发生率

连续型随机变量
正态分布
概率密度函数:
f
(
x
)
=
1
2
π
σ
2
e
−
(
x
−
μ
)
2
2
σ
2
f(x)=\frac1{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
f(x)=2πσ2
1e−2σ2(x−μ)2
期望值:
E
(
x
)
=
μ
E(x)=\mu
E(x)=μ
方差:
Var
(
X
)
=
σ
2
\operatorname{Var}(X)=\sigma^2
Var(X)=σ2
期望
期望是随机变量取值的平均,以概率为权重对随机变量进行加权求和
平均数是对一组已经观察到的样本进行统计的量
由于概率是频率随样本趋于无穷的极限,所以期望其实就是平均数随样本趋于无穷的极限,两者是通过大数定理联系起来的
- 离散型随机变量的期望值 E ( X ) \mathrm{E}(X) E(X): E ( X ) = ∑ i x i P ( X = x i ) \mathrm{E}(X)=\sum_ix_iP(X=x_i) E(X)=∑ixiP(X=xi)
- 连续型随机变量的期望值 E ( X ) \mathrm{E}(X) E(X): E ( X ) = ∫ − ∞ ∞ x f X ( x ) d x E(X)=\int_{-\infty}^\infty xf_X(x) dx E(X)=∫−∞∞xfX(x)dx
期望的性质:
- E ( X 1 + X 2 + ⋯ + X n ) = E ( X 1 ) + E ( X 2 ) + ⋯ + E ( X n ) \mathrm{E}\left(\mathrm{X}_1 +\mathrm{X}_2 + \cdots +\mathrm{X}_\mathrm{n}\right)=\mathrm{E}\left(\mathrm{X}_1 \right)+\mathrm{E}\left(\mathrm{X}_2 \right)+ \cdots+\mathrm{E}\left(\mathrm{X}_\mathrm{n} \right) E(X1+X2+⋯+Xn)=E(X1)+E(X2)+⋯+E(Xn)(无条件成立)
- E ( X 1 X 2 ⋯ X n ) = E ( X 1 ) E ( X 2 ) ⋯ E ( X n ) \mathrm{E}(X_1 X_2 \cdots X_n) = \mathrm{E}(X_1 ) \mathrm{E} (X_2 ) \cdots \mathrm{E} (X_n ) E(X1X2⋯Xn)=E(X1)E(X2)⋯E(Xn)(独立情况下成立)
方差
方差是用来衡量随机变量和其数学期望之间的偏离程度的量,方差越大,那么这一组数据的波动幅度也就越大
因为
X
X
X是随机的,所以偏离的量
X
−
E
X
X-EX
X−EX本身也是随机的,为了避免正负相互抵消,对其取平方作为偏离量,很自然方差就是该偏离量的期望,定义为:
V
a
r
(
X
)
=
E
(
X
−
E
X
)
2
=
E
(
X
2
)
−
(
E
X
)
2
\mathrm{Var(X)=E(X-EX)^2=E\left(X^2\right)-(EX)^2}
Var(X)=E(X−EX)2=E(X2)−(EX)2
假如给定一个含有
n
n
n个样本的集合,则方差计算为:
σ
2
=
∑
i
=
1
n
(
X
i
−
X
ˉ
)
2
n
−
1
\mathrm{\sigma^2=\frac{\sum_{i=1}^n\left(X_i-\bar{X}\right)^2}{n-1}}
σ2=n−1∑i=1n(Xi−Xˉ)2
之所以除以n-1而不是除以n,是因为我们是用样本去估计总体,除n-1才是统计学上的“无偏估计”,这样能使我们以较小的样本集更好的逼近总体的标准差
方差的性质:
- 常数的方差为 0 0 0
- 若 C C C为常数,则 V a r ( X + C ) = V a r ( X ) \mathrm{Var(X+C)=Var(X)} Var(X+C)=Var(X)
- 若 C C C为常数,则 V a r ( C X ) = C 2 V a r ( X ) \mathrm{Var(CX)=C^2Var(X)} Var(CX)=C2Var(X)
- 独立情况下, V a r ( X 1 + ⋯ + X n ) = V a r ( X 1 ) + ⋯ + V a r ( X n ) \mathrm{Var\left(X_1\right.+\cdots+X_n})=\mathrm{Var\left(X_1)\right.}+\cdots+\mathrm{Var\left(X_n\right)} Var(X1+⋯+Xn)=Var(X1)+⋯+Var(Xn)
标准化
标准化可以使每个样本的均值为0、标准差为1: x ′ = x − x ˉ σ \mathrm x'=\frac{\mathrm x-\bar{\mathrm x}}\sigma x′=σx−xˉ
协方差
协方差衡量两个随机变量之间的线性关系
对于两个随机变量
X
X
X和
Y
Y
Y,协方差的定义为
Cov
(
X
,
Y
)
=
E
[
(
X
−
E
(
X
)
)
(
Y
−
E
(
Y
)
)
]
=
E
(
X
Y
)
−
E
(
X
)
E
(
Y
)
\operatorname{Cov}(X,Y)=E\left[(X-E(X))(Y-E(Y))\right]=E(XY)-E(X)E(Y)
Cov(X,Y)=E[(X−E(X))(Y−E(Y))]=E(XY)−E(X)E(Y)
- 正协方差:如果 Cov ( X , Y ) > 0 \operatorname{Cov}(X,Y)>0 Cov(X,Y)>0,则表明 X X X和 Y Y Y之间存在正的线性关系
- 负协方差:如果 Cov ( X , Y ) < 0 \operatorname{Cov}(X,Y)<0 Cov(X,Y)<0,则表明 X X X和 Y Y Y之间存在负的线性关系
- 零协方差:如果 Cov ( X , Y ) = 0 \operatorname{Cov}(X,Y)=0 Cov(X,Y)=0,则表明 X X X和 Y Y Y之间没有线性关系 ⇒ \Rightarrow ⇒零协方差并不意味着 X X X和 Y Y Y完全不相关,它们可能存在非线性的关系
假设数据矩阵
X
X
X的大小为
n
×
p
n\times p
n×p,其中
n
n
n是样本数,
p
p
p是特征数,
X
X
X的每一行代表一个样本,每一列代表一个特征
给定数据矩阵
X
X
X,协方差矩阵的计算公式为:
Σ
=
1
n
−
1
X
T
X
\Sigma=\frac{1}{n-1}X^TX
Σ=n−11XTX
X
T
X
X^TX
XTX是一个
p
×
p
p\times p
p×p的矩阵,表示各特征之间的内积和

相关系数
协方差虽然能反映两个随机变量的相关程度,为了标准化这种相关性,我们通常使用相关系数(Correlation Coefficient),其定义为: ρ X , Y = Cov ( X , Y ) σ X σ Y E [ ( X − E X ) ( Y − E Y ) ] σ X σ Y = E ( X Y ) − E ( X ) E ( Y ) E ( X 2 ) − E 2 ( X ) E ( Y 2 ) − E 2 ( Y ) \rho_{X,Y}=\frac{\operatorname{Cov}(X,Y)}{\sigma_X\sigma_Y}\begin{aligned}\frac{\mathrm{E}\left[\left(\mathrm{X}-\mathrm{E}\mathrm{X}\right)\left(\mathrm{Y}-\mathrm{E}\mathrm{Y} \right)\right]}{\sigma_\mathrm{X} \sigma_\mathrm{Y}}&=\frac{\mathrm{E}\left(\mathrm{X}\mathrm{Y}\right)-\mathrm{E}\left(\mathrm{X}\right)\mathrm{E}\left(\mathrm{Y}\right)}{\sqrt{\mathrm{E}\left(\mathrm{X}^2\right)-\mathrm{E}^2\left(\mathrm{X}\right)}\sqrt{\mathrm{E}\left(\mathrm{Y}^2\right)-\mathrm{E}^2\left(\mathrm{Y}\right)}}\end{aligned} ρX,Y=σXσYCov(X,Y)σXσYE[(X−EX)(Y−EY)]=E(X2)−E2(X) E(Y2)−E2(Y) E(XY)−E(X)E(Y),其中 σ X \sigma_X σX和 σ Y \sigma_Y σY分别是 X X X和 Y Y Y的标准差,相关系数 ρ X , Y \rho_{X,Y} ρX,Y的值域为 [ − 1 , 1 ] [-1,1] [−1,1],值越接近 1 或 -1,表明 X X X和 Y Y Y之间的线性关系越强
线性组合
线性组合:设
β
,
α
1
,
α
2
,
.
.
.
,
α
n
\mathrm{\beta} , \alpha_{1} , \alpha_{2} , ..., \alpha_{\mathrm{n}}
β,α1,α2,...,αn是一组
m
m
m维向量,若存在数
k
1
,
k
2
,
.
.
.
,
k
n
\mathrm{k_{1} , k_{2} , ...,k_{n}}
k1,k2,...,kn,使得
β
=
k
1
α
1
+
k
2
α
2
+
.
.
.
+
k
n
α
n
\mathrm{\beta=k_1\alpha_1~+k_2\alpha_2~+~...~+k_n\alpha_n}
β=k1α1 +k2α2 + ... +knαn,则称
β
\beta
β是向量组
α
1
,
α
2
,
.
.
.
,
α
n
\alpha_{1} , \alpha_{2} , ..., \alpha_{\mathrm{n}}
α1,α2,...,αn的线性组合,
k
1
,
k
2
,
.
.
.
,
k
n
\mathrm{k_{1} , k_{2} , ...,k_{n}}
k1,k2,...,kn为一组组合系数
性质:
- 零向量可由任意向量组来线性表示: 0 = 0 α 1 + 0 α 2 + . . . + 0 α n \mathbf{0}=0\alpha_1+0\alpha_2+...+0\alpha_\mathrm{n} 0=0α1+0α2+...+0αn
- 向量组中任意一个向量可由向量组来线性表示: α 3 = 0 α 1 + 0 α 2 + 1 α 3 + 0 α 4 \alpha_3=0\alpha_1+0\alpha_2+1\alpha_3+0\alpha_4 α3=0α1+0α2+1α3+0α4
-
任意一个向量都可由基向量
ε
1
=
(
1
,
0
,
.
.
.
,
0
)
,
ε
2
=
(
0
,
1
,
.
.
.
,
0
)
,
.
.
.
,
ε
n
=
(
0
,
0
,
.
.
.
,
1
)
\begin{aligned}\varepsilon_1& =(1,0,...,0),\varepsilon_2 =(0,1,...,0),...,\varepsilon_\text{n} =(0,0,...,1)\end{aligned}
ε1=(1,0,...,0),ε2=(0,1,...,0),...,εn=(0,0,...,1)来线性表示:
(
1
,
2
,
3
)
=
1
×
(
1
,
0
,
0
)
+
2
×
(
0
,
1
,
0
)
+
3
×
(
0
,
0
,
1
)
(1,2,3)=1\times(1,0,0)+2\times(0,1,0)+3\times(0,0,1)
(1,2,3)=1×(1,0,0)+2×(0,1,0)+3×(0,0,1)
设 β = ( − 3 , 2 , − 4 ) , α 1 = ( 1 , 0 , 1 ) , α 2 = ( 2 , 1 , 0 ) , α 3 = ( − 1 , 1 , − 2 ) \beta = (-3,2,-4), \alpha_{1} = (1,0,1), \alpha_{2} = (2,1,0), \alpha_{3} =(-1,1,-2) β=(−3,2,−4),α1=(1,0,1),α2=(2,1,0),α3=(−1,1,−2),判断 β \beta β是否可由 α 1 , α 2 , α 3 \alpha_1,\alpha_2,\alpha_3 α1,α2,α3线性表示?

特征值和特征向量
特征向量表示变换的方向,特征值表示在每个方向上的伸缩程度

特征值分解
相似矩阵:设
A
,
B
A,B
A,B都是
n
n
n阶矩阵,若有可逆矩阵
P
P
P,使
P
−
1
A
P
=
B
\mathrm{P}^{-1}\mathrm{AP}=\mathrm{B}
P−1AP=B,则称
A
A
A与
B
B
B相似,这个过程称为相似变换,
P
P
P为相似变换矩阵
如果
A
A
A与对角矩阵
Λ
=
(
λ
1
λ
2
⋱
λ
n
)
\left.\boldsymbol{\Lambda}=\left(\begin{array}{rrrrr}\lambda_{1}&&&&\\&\lambda_{2}&&&\\&&\ddots&&\\&&&\lambda_{\mathrm{n}}&\end{array}\right.\right)
Λ=
λ1λ2⋱λn
相似,即
P
−
1
A
P
=
Λ
\mathrm{P}^{-1}\mathrm{AP}=\Lambda
P−1AP=Λ,那么
λ
1
,
λ
2
,
⋯
,
λ
n
\lambda_{1},\lambda_{2} ,\cdots ,\lambda_{\mathrm{n}}
λ1,λ2,⋯,λn是
A
A
A的
n
n
n个特征值,而
P
P
P的列向量
p
i
p_i
pi就是
A
A
A对应于特征值
λ
i
\lambda_i
λi的特征向量
把
P
P
P乘到右边,得到:
A
=
P
Λ
P
−
1
\mathrm A=\mathrm P\Lambda\mathrm P^{-1}
A=PΛP−1这个式子就是实际中经常用到的特征值分解,一个矩阵
A
A
A可以通过特征值分解得到它的特征值和特征向量
对称矩阵的特征值分解
对称矩阵:
A
T
=
A
\mathrm{A^{T}}=\mathrm{A}
AT=A
⇒
\Rightarrow
⇒对称矩阵有
N
N
N个线性无关的特征向量,且不同特征值对应的特征向量相互正交
对称矩阵一定可以相似对角化,故实对称矩阵
A
A
A可以被分解成:
A
=
P
Λ
P
−
1
=
P
Λ
P
T
\mathrm{A}=\mathrm{P} \Lambda\mathrm{P}^{-1}=\mathrm{P} \mathrm{\Lambda}\mathrm{P}^{\mathrm{T}}
A=PΛP−1=PΛPT,其中
P
P
P为正交矩阵(
P
P
T
=
E
\mathrm{PP}^{\mathrm{T}}=\mathrm{E}
PPT=E)
齐次线性方程组
齐次线性方程组是指所有常数项(即方程的右端)都等于零的线性方程组:
A
x
=
0
A\mathbf{x}=\mathbf{0}
Ax=0,其中
A
A
A是一个
m
×
n
m\times n
m×n的矩阵,
x
\mathbf{x}
x是一个
n
n
n维列向量,
0
\mathbf{0}
0是一个
m
m
m维列向量

单位向量
单位向量是指长度为1的向量,在欧几里得空间中,如果向量
u
\mathbf{u}
u满足
∥
u
∥
=
1
\|\mathbf{u}\|=1
∥u∥=1,其中
∥
u
∥
\|\mathbf{u}\|
∥u∥表示向量
u
\mathbf{u}
u的长度,则
u
\mathbf{u}
u是一个单位向量

基向量
基向量是向量空间的一组向量,通过线性组合这些向量可以表示空间中的任何向量,向量空间中的基向量通常是线性无关的
矩阵的秩
矩阵的秩(Rank)是其行向量的最大线性无关组的数量
从几何角度来看,矩阵的秩表示由矩阵的行向量生成的向量空间的维数,对于一个
3
×
3
3\times3
3×3的矩阵:
- 如果其秩为 3,表示其行向量是三维空间的基,可以生成整个三维空间
- 如果秩为 2,表示行向量位于同一平面,且可以生成一个二维平面
- 如果秩为 1,表示所有行向量都在同一条直线上

对于方阵,如果其行列式不为零,则该矩阵是满秩矩阵,即秩等于矩阵的阶数。反之,如果行列式为零,则矩阵的秩小于其阶数
最高阶非零子式
一个
k
×
k
k\times k
k×k子式是从矩阵中选取
k
k
k行和
k
k
k列形成的一个
k
×
k
k\times k
k×k方阵的行列式
最高阶非零子式是指在所有非零子式中,阶数最高的那个子式
假设有一个
3
×
3
3\times 3
3×3矩阵:
A
=
(
1
2
3
4
5
6
7
8
9
)
A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}
A=
147258369

正定矩阵
正定矩阵是一种特殊的实对称矩阵
实对称矩阵:矩阵的转置等于其自身的矩阵,对于任意
i
i
i和
j
j
j,其第
i
i
i行第
j
j
j列的元素等于第
j
j
j行第
i
i
i列的元素
一个实对称矩阵
A
A
A 被称为正定的,如果对于任意非零向量
x
x
x,都有
x
T
A
x
>
0
x^TAx>0
xTAx>0
一个实对称矩阵
A
A
A被称为半正定的,如果对于任意非零向量
x
x
x,都有
x
T
A
x
≥
0
x^TAx\geq0
xTAx≥0
正交矩阵
正交矩阵的逆矩阵和转置矩阵是相同的
一个正交矩阵
Q
Q
Q满足下列条件:
- 它是一个方阵(即行数等于列数)
- 它的每一列都是单位向量,并且相互正交
正交基
一个向量组
{
u
1
,
u
2
,
…
,
u
n
}
\{\mathbf{u}_1,\mathbf{u}_2,\ldots,\mathbf{u}_n\}
{u1,u2,…,un}是正交基,如果组内的任意两个向量都是正交的,即
u
i
⋅
u
j
=
0
\mathbf{u}_{i}\cdot\mathbf{u}_{j}=0
ui⋅uj=0(对于所有
i
≠
j
i\neq j
i=j),如果这些向量还都是单位向量,则称它们是正交规范基
在三维空间中,标准基向量
{
e
1
,
e
2
,
e
3
}
\{\mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3\}
{e1,e2,e3}是一个正交规范基:
e
1
=
(
1
,
0
,
0
)
,
e
2
=
(
0
,
1
,
0
)
,
e
3
=
(
0
,
0
,
1
)
\mathbf{e}_1=(1,0,0),\quad\mathbf{e}_2=(0,1,0),\quad\mathbf{e}_3=(0,0,1)
e1=(1,0,0),e2=(0,1,0),e3=(0,0,1)
逆矩阵
假如说,矩阵
A
A
A是逆时针旋转90°的变换,则
A
−
1
A^{-1}
A−1是顺时针旋转90°的变换
如果矩阵
A
A
A可逆,则
A
−
1
=
A
∗
∣
∣
A
∣
∣
A^{-1}=\frac{A^{*}}{||A||}
A−1=∣∣A∣∣A∗(
∣
∣
A
∣
∣
=
det
(
A
)
||A||=\det(A)
∣∣A∣∣=det(A),即矩阵的行列式)
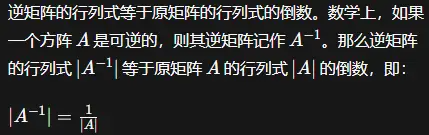
伴随矩阵
伴随矩阵
A
∗
A^{*}
A∗
余子式:
A
A
A关于第
i
i
i行第
j
j
j列的余子式(记作
M
i
j
M_{ij}
Mij)是去掉
A
A
A的第
i
i
i行第
j
j
j列之后得到的
(
n
−
1
)
×
(
n
−
1
)
(n-1)\times (n-1)
(n−1)×(n−1)矩阵的行列式
代数余子式:
A
A
A关于第
i
i
i行第
j
j
j列的代数余子式(记作
C
i
j
C_{ij}
Cij)为
(
−
1
)
i
+
j
M
i
j
(-1)^{i+j}M_{ij}
(−1)i+jMij
余子矩阵:
A
A
A的余子矩阵是一个
n
×
n
n\times n
n×n的矩阵
C
C
C,使得第
i
i
i行第
j
j
j列的元素是
A
A
A关于第
i
i
i行第
j
j
j列的代数余子式
伴随矩阵:矩阵
A
A
A的伴随矩阵是
A
A
A的余子矩阵的转置矩阵
奇异值分解
特征分解只适用于方阵,奇异值分解SVD适用于任意矩阵分解
从相似对角化的的定义可以看到,我们可以把一个复杂的矩阵
A
A
A变成一个很简单的对角矩阵,而这个对角矩阵也同样保留了原来矩阵的特征,且变换的矩阵
P
P
P就是
A
A
A的特征向量组成的矩阵
但是注意,不是每一个矩阵都能与对角矩阵相似,首先注意到
P
P
P必须是可逆的,而
P
P
P又是特征向量组成
⇒
\Rightarrow
⇒当且仅当
A
A
A有
n
n
n个线性无关的特征向量时,
A
A
A才能相似对角化
奇异值分解就像是把一个复杂的玩具分解成几个更简单的小玩具,然后用这些小玩具重新拼装成原来的玩具
假设我们有一个
m
×
n
m\times n
m×n的矩阵
A
A
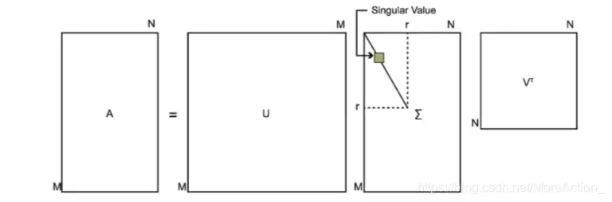
A,,奇异值分解把它分解成三个矩阵:
A
=
U
Σ
V
T
A=U\Sigma V^{T}
A=UΣVT
- 矩阵 U U U: m × m m\times m m×m的正交矩阵,其中的列向量 u 1 ⃗ , u 2 ⃗ , … , u m ⃗ \vec{\mathrm{u}_1},\vec{\mathrm{u}_2},\ldots,\vec{\mathrm{u}_m} u1 ,u2 ,…,um 是 A A T AA^T AAT的特征向量,称为矩阵 A A A的左奇异向量
- 矩阵数学 Σ \Sigma Σ: m × n m\times n m×n的矩阵,除了主对角线上的元素以外全为0,主对角线上的元素 σ i \sigma_i σi称为奇异值, σ i = λ i \sigma_{\mathrm{i}}=\sqrt{\lambda_{\mathrm{i}}} σi=λi , λ i \lambda_i λi是 A A T AA^T AAT的特征值
- 矩阵
V
T
V^T
VT:
n
×
n
n\times n
n×n的正交矩阵,其中的列向量
v
⃗
1
,
v
⃗
2
,
…
,
v
⃗
m
\vec{\mathrm{v}}_{1} , \vec{\mathrm{v}}_{2} ,\ldots, \vec{\mathrm{v}}_{\mathrm{m}}
v
1,v
2,…,v
m是
A
T
A
A^TA
ATA的特征向量,称为矩阵
A
A
A的右奇异向量
奇异值在矩阵中是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说,我们可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说: A m × n = U m × m Σ m × n V n × n T ≈ U m × k Σ k × k V k × n T \mathrm A_{\mathrm m\times\mathrm n}=\mathrm U_{\mathrm m\times\mathrm m}\Sigma_{\mathrm m\times\mathrm n}\mathrm V_{\mathrm n\times\mathrm n}^{\mathrm T}\approx\mathrm U_{\mathrm m\times\mathrm k}\Sigma_{\mathrm k\times\mathrm k}\mathrm V_{\mathrm k\times\mathrm n}^{\mathrm T} Am×n=Um×mΣm×nVn×nT≈Um×kΣk×kVk×nT,其中,k是一个远小于m、n的数。SVD具有的这种特性可以用于PCA降维、数据压缩和去噪等
A A T AA^T AAT是对称矩阵

主成分分析
假设我们有一组二维数据
(
x
,
y
)
(x,y)
(x,y),它的分布如下:
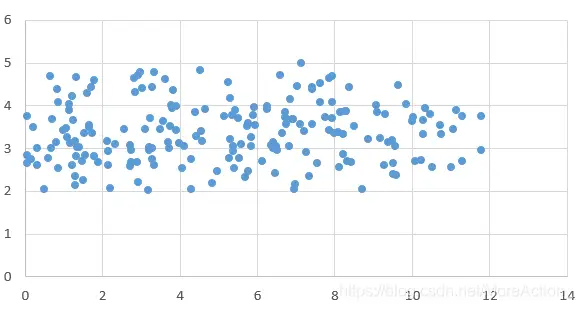
可以看到,数据在x轴上的变化大,而在y轴变化小,变化小意味着数据在这个特征上没有太大的差异,因此它包含的信息就比较少,那么我们就可以认为它是不重要的或者是噪音,从而可以直接将这个维度上的数据舍去,只用x轴上的数据来代替
那么假如数据是这样分布的呢?

这个图我们就不太好看出到底是谁比较重要了,因为x和y变化都比较大,那么就不能降维了吗?非也,假如我们旋转一下坐标系
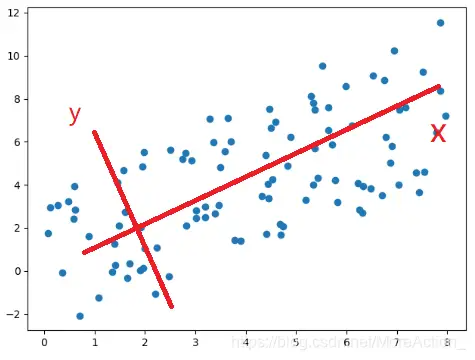
从这个例子也可以看到,数据本身的具体数值其实是不重要的,重要的是数据之间的关系,数据的整体分布。原来的数据是在
E
E
E坐标系下,然后我们换了一个坐标系来表示,本质上相当于对数据进行了一次正交变换(从数学公式看),在新的坐标系下,我们能更清楚的看到数据的特点
PCA的目标是将原始数据转换到一个新的坐标系中,这个新坐标系的轴(主成分)是数据方差最大的方向
主成分是在数据集中找到方差最大的方向(即主成分),然后将数据投影到这些方向上
方差最大化:每个主成分方向上数据的方差最大,这意味着这个方向上数据分布最广,包含最多的信息
正交性:不同主成分之间是相互正交的,即它们彼此垂直且不相关
PCA的步骤:
- 数据标准化:将每个特征的均值变为零,方差变为一,确保每个特征对主成分的贡献是均衡的 ⇒ \Rightarrow ⇒ 标准化数据 = X − μ σ \text{标准化数据}=\frac{X-\mu}\sigma 标准化数据=σX−μ
- 计算协方差矩阵:协方差矩阵描述了不同特征之间的线性关系 ⇒ \Rightarrow ⇒ Σ = 1 n − 1 X T X \Sigma=\frac{1}{n-1}X^TX Σ=n−11XTX,其中, Σ \Sigma Σ是协方差矩阵, X X X是标准化后的数据矩阵, n n n是样本数量
- 特征值分解:对协方差矩阵进行特征值分解,得到特征值和特征向量 ⇒ \Rightarrow ⇒ Σ = V Λ V T \Sigma=V\Lambda V^{T} Σ=VΛVT,其中, V V V是特征向量矩阵, Λ \Lambda Λ是对角矩阵,对角线上的元素是特征值
- 选择前 k k k个主成分:选择特征值最大的 k k k个特征向量,作为新的特征子空间的基,这些特征向量就是主成分;特征值代表了每个特征向量方向上的方差大小,特征值越大,表示这个方向上的方差越大,包含的信息越多
- 变换数据:用选择的 k k k个主成分对原始数据进行变换,得到降维后的数据 Y = X P Y=XP Y=XP,其中, Y Y Y是降维后的数据矩阵, P P P是由选择的 k k k个特征向量构成的矩阵

参考文献
1、ChatGPT3.5、ChatGPT4.0、ChatGPT4o
2、概率分布介绍—泊松分布:https://blog.csdn.net/weixin_44633882/article/details/120313676
3、相关系数——皮尔逊相关系数:https://blog.csdn.net/MoreAction_/article/details/106195689
4、《线性代数》教学视频 宋浩老师:https://www.bilibili.com/video/BV1aW411Q7x1?p=1&vd_source=8469f059ce75462e1674032ec0bfc23a
5、一文读懂特征值分解EVD与奇异值分解SVD:https://blog.csdn.net/MoreAction_/article/details/107318158
6、一文让你彻底搞懂主成成分分析PCA的原理及代码实现:https://blog.csdn.net/MoreAction_/article/details/107463336