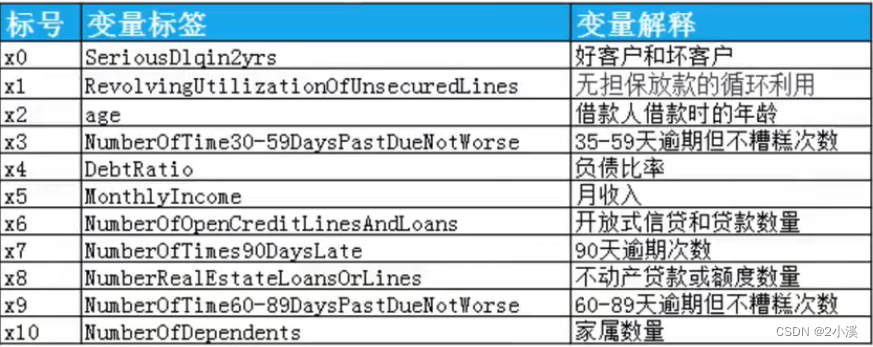
1 数据预处理数据
数据来源于Kaggle的Give Me Some Credit,包括25万条个人财务情况的样本数据
1.1 导包读数据
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
import seaborn as sns
from scipy import stats
import copy
%matplotlib inline读数据
# 读取数据
train_data = pd.read_csv('cs-training.csv')
# 选择除了第一列以外的所有列
train_data = train_data.iloc[:,1:]
# 查看数据的基本信息
train_data.info()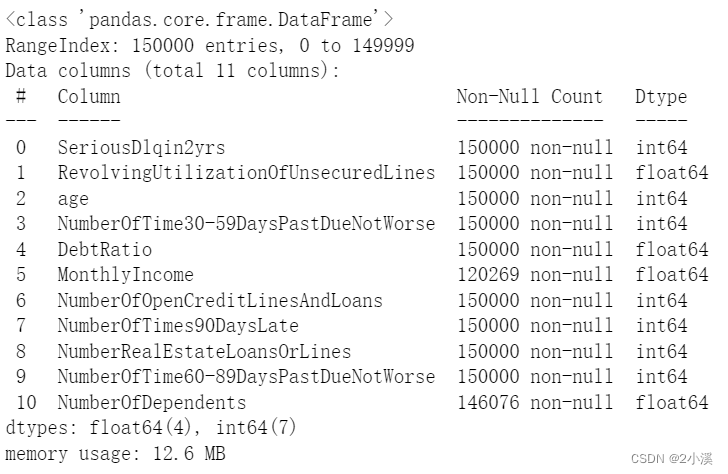
1.2 缺失值处理
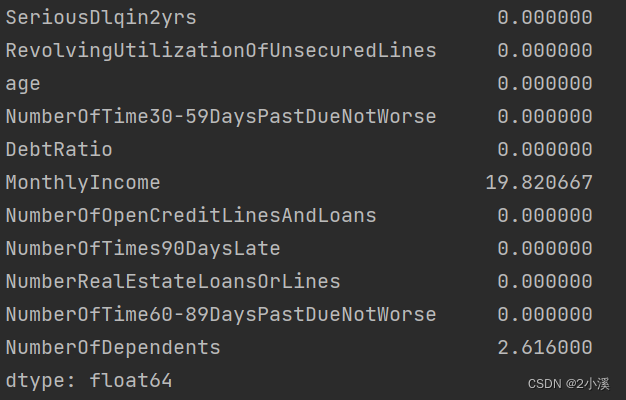
查看数据缺失率
# 计算每列的缺失值数量
missing_values = train_data.isnull().sum()
# 计算每列的缺失率
missing_rate = (missing_values / len(train_data)) * 100
# 输出缺失率
print(missing_rate)月收入和家属人数两个变量的缺失值占比分别为19.82%、2.62%
缺失较多的月收入,根据变量之间的相关关系,采用随机森林法填补缺失值
缺失较少的NumberOfDependts,对总体模型不会造成太大影响,直接删除缺失样本
# 假设已经按照需求重新排列了列
mData = train_data.iloc[:,[5,0,1,2,3,4,6,7,8,9]]
# 根据MonthlyIncome列是否有缺失值分割数据
train_known = mData[mData.MonthlyIncome.notnull()]
train_unknown = mData[mData.MonthlyIncome.isnull()]
# 使用Pandas的iloc方法来提取特征和目标变量
# 注意:iloc是基于整数位置的,所以这里的0和1对应重新排列后的列位置
train_X_known = train_known.iloc[:, 1:] # 特征,从第二列开始到最后一列
train_y_known = train_known.iloc[:, 0] # 目标变量,第一列
# 训练随机森林回归模型
rfr = RandomForestRegressor(random_state=0, n_estimators=200, max_depth=3, n_jobs=-1)
rfr.fit(train_X_known, train_y_known)
# 使用模型预测train_unknown中的Missing MonthlyIncome值
train_X_unknown = train_unknown.iloc[:, 1:] # 特征,从第二列开始到最后一列
predicted_y = rfr.predict(train_X_unknown).round(0)
# 将预测值填充回原DataFrame的相应位置
train_data.loc[train_unknown.index, 'MonthlyIncome'] = predicted_y
# 删除含有缺失值的行
train_data = train_data.dropna()
# 删除重复的行
train_data = train_data.drop_duplicates()1.3 处理异常值
异常值通常用箱型图来判断
# 处理异常值
# 选择特定的列来绘制箱线图
train_box = train_data.iloc[:,[3,7,9]]
# 创建一个新的图形
plt.figure(figsize=(10, 5)) # 可以调整图形大小以适应您的需要
# 绘制箱线图
train_box.boxplot()
# 设置图形标题和坐标轴标签(如果需要)
plt.title('Box Plot of Selected Columns')
plt.ylabel('Values')
# 显示图形
plt.show()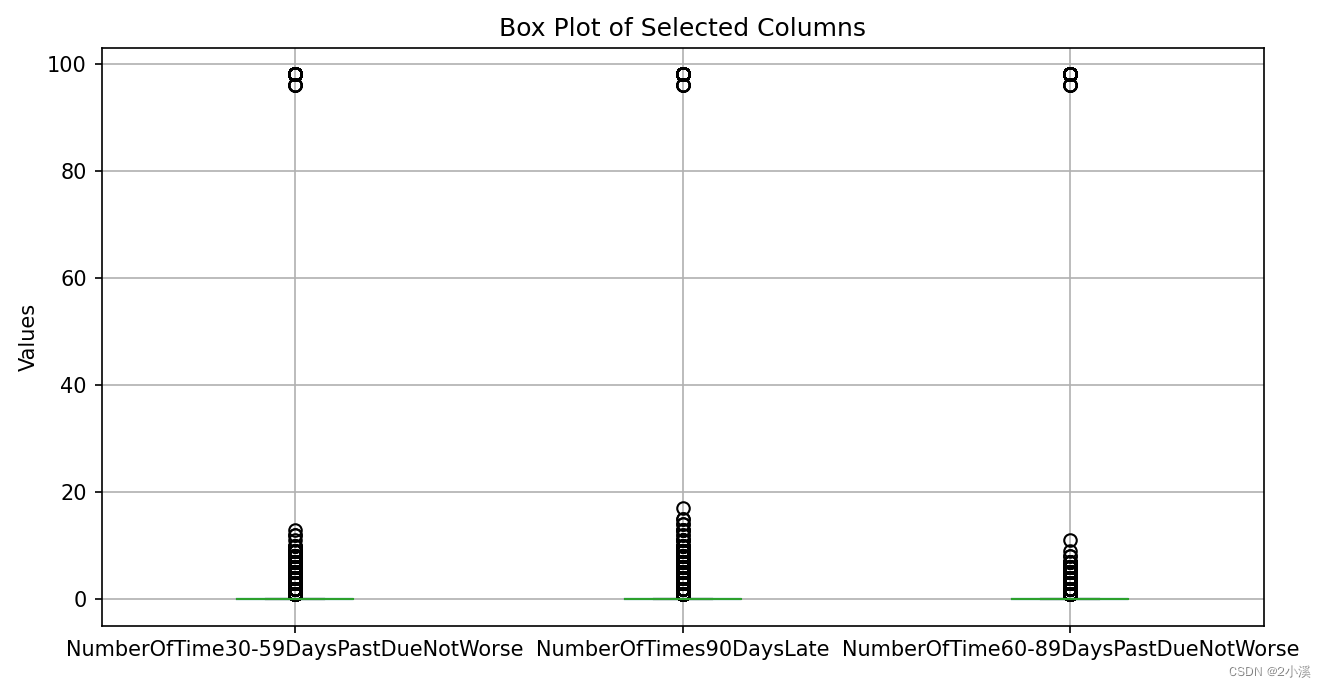
查看全部列
train_box = train_data.iloc[:, :]
 删除变量NumberOfTime30-59DaysPastDueNotWorse、NurmberOfTimes90DaysLate、NumberOfTime60-89DaysPastDueNotWorse的异常值,剔除其中一个变量的异常值,其他变量的异常值也会相应被剔除。
删除变量NumberOfTime30-59DaysPastDueNotWorse、NurmberOfTimes90DaysLate、NumberOfTime60-89DaysPastDueNotWorse的异常值,剔除其中一个变量的异常值,其他变量的异常值也会相应被剔除。
客户的年龄为0时,通常认为该值为异常值,直接剔除。
# 舍弃age为0
train_data = train_data[train_data['NumberOfTime30-59DaysPastDueNotWorse']<90]
train_data = train_data[train_data.age>0]
#使好客户为1,违约客户为0
train_data['SeriousDlqin2yrs'] = 1-train_data['SeriousDlqin2yrs'] 1.4 数据切分
为了验证模型性能,将数据切分化为训练集和测试集,测试集取原数据的30%。
from sklearn.model_selection import train_test_split
# 假设 train_data 是一个 Pandas DataFrame,将其分为特征和目标变量
y = train_data.iloc[:, 0] # 目标变量,假设在第一列
X = train_data.iloc[:, 1:] # 特征变量,从第二列到最后一列
# 使用 train_test_split 来分割数据为训练集和测试集
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.3, random_state=0)
# 使用 Pandas 的 concat 函数将训练集和测试集的目标变量和特征变量合并回 DataFrame
ntrain_data = pd.concat([pd.DataFrame(train_y), train_X], axis=1)
ntest_data = pd.concat([pd.DataFrame(test_y), test_X], axis=1)
# 注意:将 train_y 和 test_y 转换为 DataFrame 是为了确保它们与 train_X 和 test_X 的索引对齐
# 如果 train_y 和 test_y 是 Series,并且它们的索引与 train_X 和 test_X 的索引一致,那么可以直接合并2 探索性分析
在建立模型之前,一般会对现有的数据进行 探索性数据分析(Exploratory Data Analysis) 。 EDA是指对已有的数据(特别是调查或观察得来的原始数据)在尽量少的先验假定下进行探索。
常用的探索性数据分析方法有:直方图、散点图和箱线图等。
年龄的分布大致呈正态分布,符合统计分析假设。
age = ntrain_data['age']
sns.distplot(age)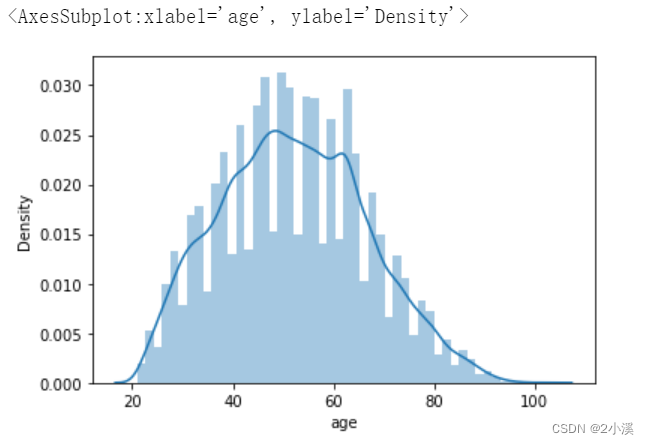
月收入的分布也大致呈正态分布。
mi = ntrain_data[['MonthlyIncome']]
sns.distplot(mi)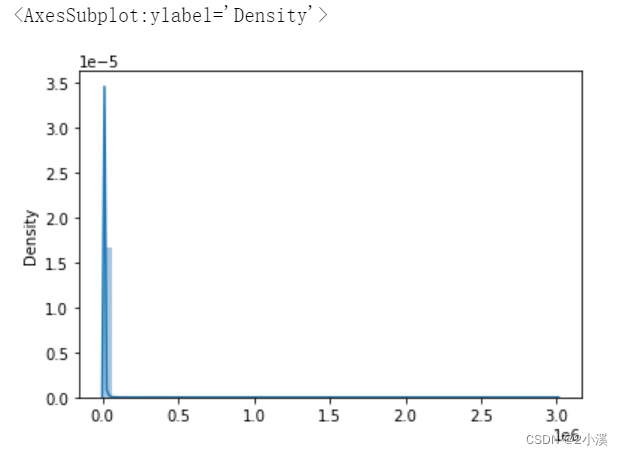
3 变量选择
3.1 分箱处理
3.1.1 连续变量最优分段
定义自动分箱函数,单调分箱,是基于IV(Information Value)和WOE(Weight of Evidence)两个指标来进行的。
WOE是一种衡量某个分箱中好坏样本分布相对于总样本分布的指标。它通过对数转换来量化这种分布差异,使得WOE值能够直观地反映该分箱对于区分好坏样本的能力。
IV则是基于WOE计算得出的一个汇总指标,用于衡量整个特征(经过分箱处理后)对于预测目标变量的信息量。IV值越高,说明该特征对于预测目标变量的贡献越大。
在单调分箱的过程中,会同时考虑WOE和IV两个指标。一方面,要确保分箱后的WOE值呈现单调性,这有助于保证模型的可解释性和单调性约束;另一方面,也要关注IV值,以评估分箱操作是否有效地提高了特征的预测能力。
def mono_bin(Y, X, n=10):
r = 0
good=Y.sum()
bad=Y.count()-good
while np.abs(r) < 1:
d1 = pd.DataFrame({"X": X, "Y": Y, "Bucket": pd.qcut(X, n)})
d2 = d1.groupby('Bucket', as_index = True)
r, p = stats.spearmanr(d2.mean().X, d2.mean().Y)
n = n - 1
d3 = pd.DataFrame(d2.X.min(), columns = ['min'])
d3['min']=d2.min().X
d3['max'] = d2.max().X
d3['sum'] = d2.sum().Y
d3['total'] = d2.count().Y
d3['rate'] = d2.mean().Y
d3['woe']=np.log((d3['rate']/good)/((1-d3['rate'])/bad))
d3['goodattribute']=d3['sum']/good
d3['badattribute']=(d3['total']-d3['sum'])/bad
iv=((d3['goodattribute']-d3['badattribute'])*d3['woe']).sum()
d4 = (d3.sort_values(by='min')).reset_index(drop=True)
# d4 = (d3.sort_index(by = 'min')).reset_index(drop=True)
woe=list(d4['woe'].round(3))
cut=[]
cut.append(float('-inf'))
for i in range(1,n+1):
qua=X.quantile(i/(n+1))
cut.append(round(qua,4))
cut.append(float('inf'))
return d4,iv,cut,woe对于 RevolvingUtilizationOfUnsecuredLines、age、DebtRatio和MonthlyIncome使用这种方式进行分类。连续变量离散化,最优分段。
x1_d,x1_iv,x1_cut,x1_woe = mono_bin(train_y,train_X.RevolvingUtilizationOfUnsecuredLines,n=10)
x2_d,x2_iv,x2_cut,x2_woe = mono_bin(train_y,train_X.age,n=10)
x4_d,x4_iv,x4_cut,x4_woe = mono_bin(train_y,train_X.DebtRatio,n=20)
x5_d,x5_iv,x5_cut,x5_woe = mono_bin(train_y,train_X.MonthlyIncome,n=10)查看分箱结果
# 打印RevolvingUtilizationOfUnsecuredLines的分箱结果
print("RevolvingUtilizationOfUnsecuredLines分箱结果:")
print("分布:\n", x1_d)
print("信息价值:", x1_iv)
print("分箱边界:", x1_cut)
print("权重证据:", x1_woe) 
print("age分箱结果:")
print("分布:\n", x2_d)
print("信息价值:", x2_iv)
print("分箱边界:", x2_cut)
print("权重证据:", x2_woe)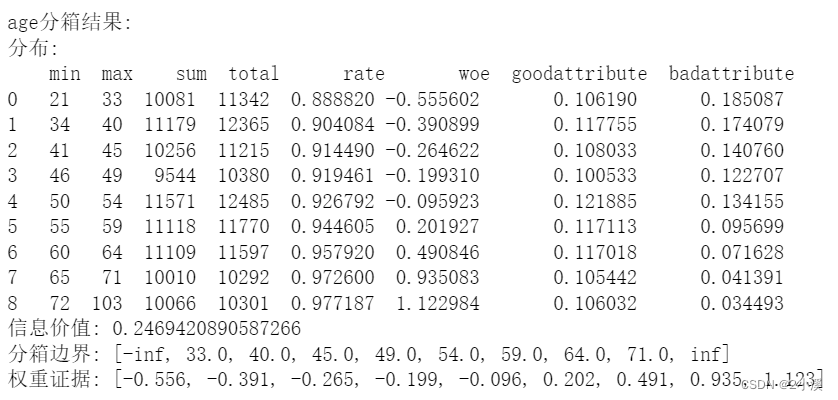
print("MonthlyIncome分箱结果:")
print("分布:\n", x5_d)
print("信息价值:", x5_iv)
print("分箱边界:", x5_cut)
print("权重证据:", x5_woe)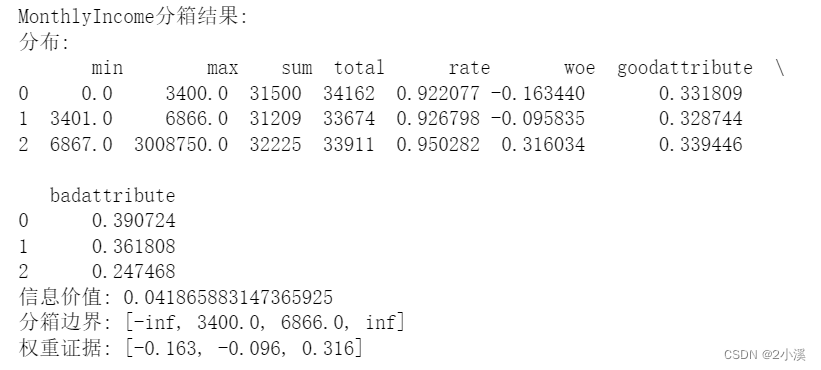
3.1.2 不能最优分箱的变量
其他不能最优分箱的变量使用人工选择的方式进行,自定义分箱,同时计算WOE(Weight of Evidence)和 IV(Information Value)。
pinf = float('inf') # 正无穷大
ninf = float('-inf') # 负无穷大
cutx3 = [ninf, 0, 1, 3, 5, pinf]
cutx6 = [ninf, 1, 2, 3, 5, pinf]
cutx7 = [ninf, 0, 1, 3, 5, pinf]
cutx8 = [ninf, 0,1,2, 3, pinf]
cutx9 = [ninf, 0, 1, 3, pinf]
cutx10 = [ninf, 0, 1, 2, 3, 5, pinf]定义计算woe的函数
def woe_value(d1):
d2 = d1.groupby('Bucket', as_index = True)
good=train_y.sum()
bad=train_y.count()-good
d3 = pd.DataFrame(d2.X.min(), columns = ['min'])
d3['min']=d2.min().X
d3['max'] = d2.max().X
d3['sum'] = d2.sum().Y
d3['total'] = d2.count().Y
d3['rate'] = d2.mean().Y
d3['woe'] = np.log((d3['rate']/good)/((1-d3['rate'])/bad))
d3['goodattribute']=d3['sum']/good
d3['badattribute']=(d3['total']-d3['sum'])/bad
iv=((d3['goodattribute']-d3['badattribute'])*d3['woe']).sum()
d4 = (d3.sort_values(by='min')).reset_index(drop=True)
# d4 = (d3.sort_index(by = 'min')).reset_index(drop=True)
woe=list(d4['woe'].round(3))
return d4,iv,woe
创建一个新的DataFrame d1,根据列X(来自train_X的某个特征)的值将其分为不同的桶(Bucket),并计算每个桶的WOE(Weight of Evidence)值和相关统计信息。
3:NumberOftime30-59DaysPastDueNotNorse
# train_X['NumberOfTime30-59DaysPastDueNotWorse'] 是特征列
# train_y 是目标列(好坏客户的标签)
# 创建一个新的DataFrame,包含特征X和目标Y
d1 = pd.DataFrame({"X": train_X['NumberOfTime30-59DaysPastDueNotWorse'], "Y": train_y})
# 简单地将X列的值复制到新列Bucket中
d1['Bucket'] = d1['X']
d1_x1 = d1.loc[(d1['Bucket']<=0)]
d1_x1.loc[:,'Bucket']="(-inf,0]"
# 根据Bucket列的值创建了不同的子集
# 为每个子集的Bucket列设置了新的字符串值,这些值描述了每个子集的数值范围
d1_x2 = d1.loc[(d1['Bucket']>0) & (d1['Bucket']<= 1)]
d1_x2.loc[:,'Bucket'] = "(0,1]"
d1_x3 = d1.loc[(d1['Bucket']>1) & (d1['Bucket']<= 3)]
d1_x3.loc[:,'Bucket'] = "(1,3]"
d1_x4 = d1.loc[(d1['Bucket']>3) & (d1['Bucket']<= 5)]
d1_x4.loc[:,'Bucket'] = "(3,5]"
d1_x5 = d1.loc[(d1['Bucket']>5)]
d1_x5.loc[:,'Bucket']="(5,+inf)"
# 合并所有子集,将所有子集合并回一个DataFrame
d1 = pd.concat([d1_x1,d1_x2,d1_x3,d1_x4,d1_x5])
# 调用了woe_value函数,并传入了合并后的DataFrame d1。
# 返回每个桶的WOE值(x3_woe)、信息价值(IV,x3_iv)和其他描述性统计信息(x3_d)
x3_d,x3_iv,x3_woe= woe_value(d1)
# 定义桶的边界
# 定义了一个列表,它描述了Bucket列的数值范围边界。这些边界与前面为子集设置的字符串值相对应
x3_cut = [float('-inf'),0,1,3,5,float('+inf')]6:NumberOfOpenCreditLinesAndLoans
d1 = pd.DataFrame({"X": train_X['NumberOfOpenCreditLinesAndLoans'], "Y": train_y})
d1['Bucket'] = d1['X']
d1_x1 = d1.loc[(d1['Bucket']<=0)]
d1_x1.loc[:,'Bucket']="(-inf,0]"
d1_x2 = d1.loc[(d1['Bucket']>0) & (d1['Bucket']<= 1)]
d1_x2.loc[:,'Bucket'] = "(0,1]"
d1_x3 = d1.loc[(d1['Bucket']>1) & (d1['Bucket']<= 3)]
d1_x3.loc[:,'Bucket'] = "(1,3]"
d1_x4 = d1.loc[(d1['Bucket']>3) & (d1['Bucket']<= 5)]
d1_x4.loc[:,'Bucket'] = "(3,5]"
d1_x5 = d1.loc[(d1['Bucket']>5)]
d1_x5.loc[:,'Bucket']="(5,+inf)"
d1 = pd.concat([d1_x1,d1_x2,d1_x3,d1_x4,d1_x5])
x6_d,x6_iv,x6_woe= woe_value(d1)
x6_cut = [float('-inf'),0,1,3,5,float('+inf')]7:NumberOfTimes90DaysLate
8:NumberRealEstateLoansOrLines
9:NumberOfTime60-89DaysPastDueNotWorse
10:NumberOfDependents
3.1.3 检查变量之间相关性
corr = train_data.corr()
xticks = ['x0','x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']
yticks = list(corr.index)
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
sns.heatmap(corr, annot=True, cmap='rainbow', ax=ax1, annot_kws={'size': 5, 'color': 'blue'})
ax1.set_xticklabels(xticks, rotation=0, fontsize=10)
ax1.set_yticklabels(yticks, rotation=0, fontsize=10)
plt.show()
可以看到 NumberOfTime30-59DaysPastDueNotWorse, NumberOfOpenCreditLinesAndLoans和NumberOfTime60-89DaysPastDueNotWorse这三个特征对于所要预测的值有较强的相关性。
3.2 查看各变量IV值
根据各变量的IV值来选择对数据处理有好效果的变量
# 查看各变量IV值
informationValue = []
informationValue.append(x1_iv)
informationValue.append(x2_iv)
informationValue.append(x3_iv)
informationValue.append(x4_iv)
informationValue.append(x5_iv)
informationValue.append(x6_iv)
informationValue.append(x7_iv)
informationValue.append(x8_iv)
informationValue.append(x9_iv)
informationValue.append(x10_iv)
informationValue
index=['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']
index_num = range(len(index))
ax=plt.bar(index_num,informationValue,tick_label=index)
plt.show()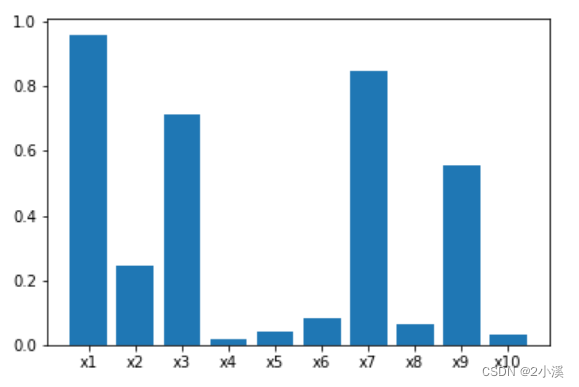
通过IV值判断变量预测能力的标准是:
< 0.02: unpredictive
0.02 to 0.1: weak
0.1 to 0.3: medium
0.3 to 0.5: strong
> 0.5: suspicious
可以看到,对于X4,X5,X6,X8,以及X10而言,IV值都比较低,因此可以舍弃这些预测能力较差的特征。
查看分箱结果
4 模型分析
4.1 WOE转换
将所有的需要的特征woe化,并将不需要的特征舍弃,仅保留WOE转码后的变量
def trans_woe(var,var_name,x_woe,x_cut):
woe_name = var_name + '_woe'
for i in range(len(x_woe)):
if i == 0:
var.loc[(var[var_name]<=x_cut[i+1]),woe_name] = x_woe[i]
elif (i>0) and (i<= len(x_woe)-2):
var.loc[((var[var_name]>x_cut[i])&(var[var_name]<=x_cut[i+1])),woe_name] = x_woe[i]
else:
var.loc[(var[var_name]>x_cut[len(x_woe)-1]),woe_name] = x_woe[len(x_woe)-1]
return var
x1_name = 'RevolvingUtilizationOfUnsecuredLines'
x2_name = 'age'
x3_name = 'NumberOfTime30-59DaysPastDueNotWorse'
x7_name = 'NumberOfTimes90DaysLate'
x9_name = 'NumberOfTime60-89DaysPastDueNotWorse'
train_X = trans_woe(train_X,x1_name,x1_woe,x1_cut)
train_X = trans_woe(train_X,x2_name,x2_woe,x2_cut)
train_X = trans_woe(train_X,x3_name,x3_woe,x3_cut)
train_X = trans_woe(train_X,x7_name,x7_woe,x7_cut)
train_X = trans_woe(train_X,x9_name,x9_woe,x9_cut)查看 train_X DataFrame 的最后五列
train_X = train_X.iloc[:,-5:]
print(train_X)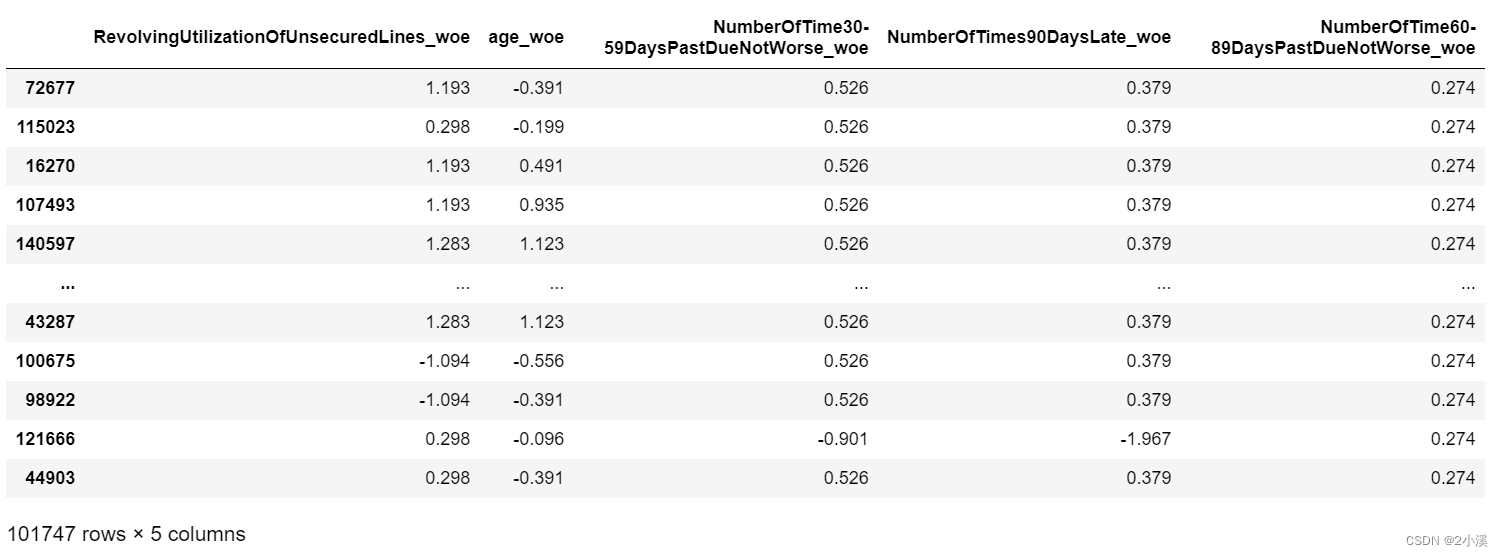
4.2 模型建立
调用STATSMODEL包来建立逻辑回归模型
# 调用STATSMODEL包来建立逻辑回归模型
import statsmodels.api as sm
# 添加常数项。逻辑回归模型需要一个常数项(通常称为截距)来估计回归方程
X1 = sm.add_constant(train_X)
# 使用train_y(训练数据的标签)和X1(带有常数项的特征矩阵)来创建一个逻辑回归模型实例
logit = sm.Logit(train_y,X1)
# 拟合模型
# fit()方法执行了最大似然估计来估计模型的参数(包括截距和系数)
result = logit.fit()
# 打印出模型的摘要,包括每个系数的估计值、标准误差、z值、p值以及模型的R-squared值、对数似然值等信息
print(result.summary())
记住这个coe每个系数的估计值,后面要用到
4.2 模型检验
模型建立后,导入测试集的数据,画出ROC曲线判断模型的准确性
4.2.1 对测试集进行woe转化
test_X = trans_woe(test_X,x1_name,x1_woe,x1_cut)
test_X = trans_woe(test_X,x2_name,x2_woe,x2_cut)
test_X = trans_woe(test_X,x3_name,x3_woe,x3_cut)
test_X = trans_woe(test_X,x7_name,x7_woe,x7_cut)
test_X = trans_woe(test_X,x9_name,x9_woe,x9_cut)
test_X = test_X.iloc[:,-5:]
print(test_X)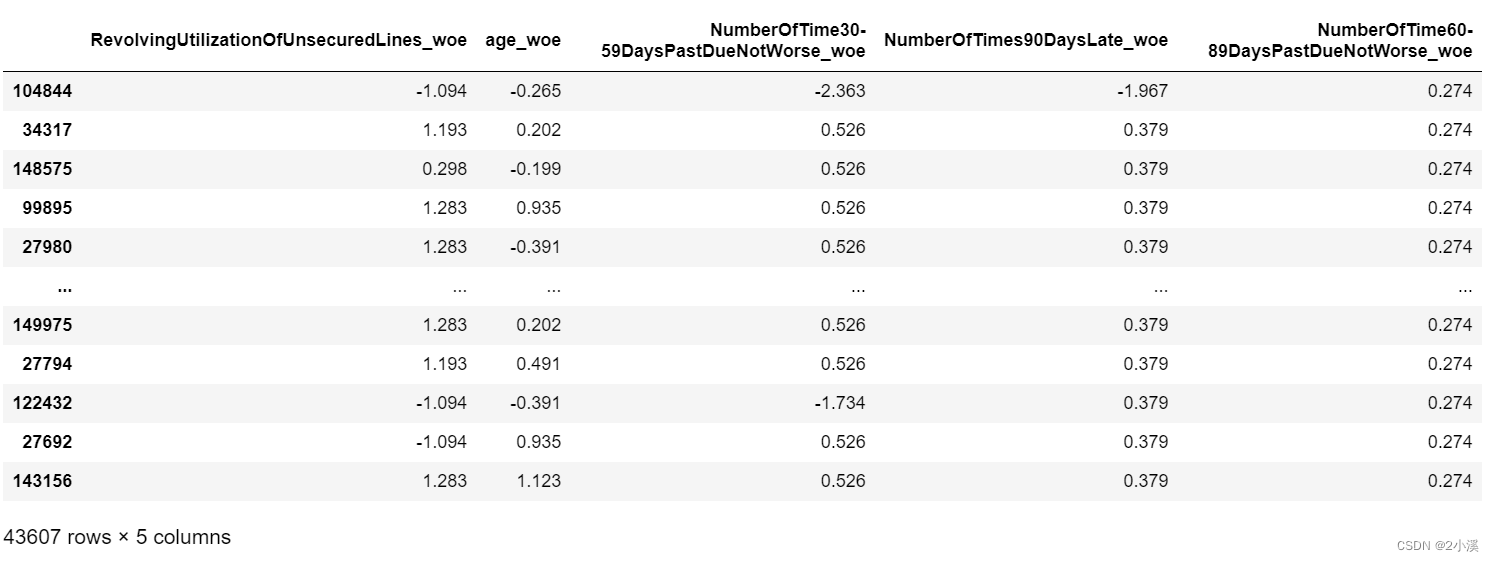
4.2.2 拟合模型,画出ROC曲线得到AUC值
通过ROC曲线和AUC值来评估模型的似合能力
sklearn.metrics自动计算ROC和AUC
# 拟合模型,画ROC曲线,得AUC值
from sklearn import metrics
X3 = sm.add_constant(test_X)
resu = result.predict(X3)
fpr, tpr, threshold = metrics.roc_curve(test_y, resu)
rocauc = metrics.auc(fpr, tpr)
plt.plot(fpr, tpr, 'b', label='AUC = %0.2f' % rocauc)
plt.legend(loc='lower right')
plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.ylabel('TPR')
plt.xlabel('FPR')
plt.show()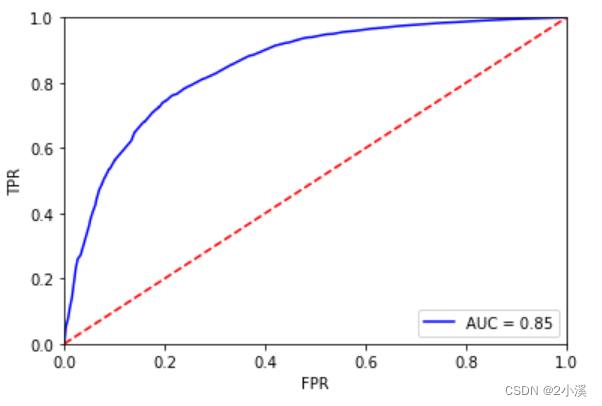
可以看到,AUC=0.85,是可以接受的。
5 建立评分卡
完成了建模相关的工作,并用ROC曲线验证了模型的预测能力
将Logistic模型转换为标准评分卡的形式
5.1 评分标准
依据资料:
a=log(p_good/P_bad)
Score = offset + factor * log(odds)
在建立标准评分卡之前,需要选取几个评分卡参数:基础分值、 PDO(比率翻倍的分值)和好坏比。 这里,取600分为基础分值,PDO为20 (每高20分好坏比翻一倍),好坏比取20。
5.2 计算分数
# 定义 p 和 q
p = 20 / np.log(2)
q = 600 - 20 * np.log(20) / np.log(2)
# 定义 get_score 函数
def get_score(coe, woe, factor):
scores = []
for w in woe:
score = round(coe * w * factor, 0)
scores.append(score)
return scores
# 定义 x_coe 列表
x_coe = [2.6084, 0.6327, 0.5151, 0.5520, 0.5747, 0.4074]
# 计算基础分数 baseScore
baseScore = round(q + p * x_coe[0], 0) x_coe是之前逻辑回归模型得到的系数。
最后BaseScore等于589分。
计算各项分数
x1_score = get_score(x_coe[1], x1_woe, p)
x2_score = get_score(x_coe[2], x2_woe, p)
x3_score = get_score(x_coe[3], x3_woe, p)
x7_score = get_score(x_coe[4], x7_woe, p)
x9_score = get_score(x_coe[5], x9_woe, p)
5.3 建立评分卡
根据前面的分箱结果和得到的分数,建立评分卡
score = [[23.0, 22.0, 5.0, -20.0],
[-8.0, -6.0, -4.0, -3.0, -1.0, 3.0, 7.0, 14.0, 17.0],
[8.0, -14.0, -28.0, -38.0, -43.0],
[6.0, -33.0, -46.0, -53.0, -51.0],
[3.0, -22.0, -32.0, -35.0, -31.0]]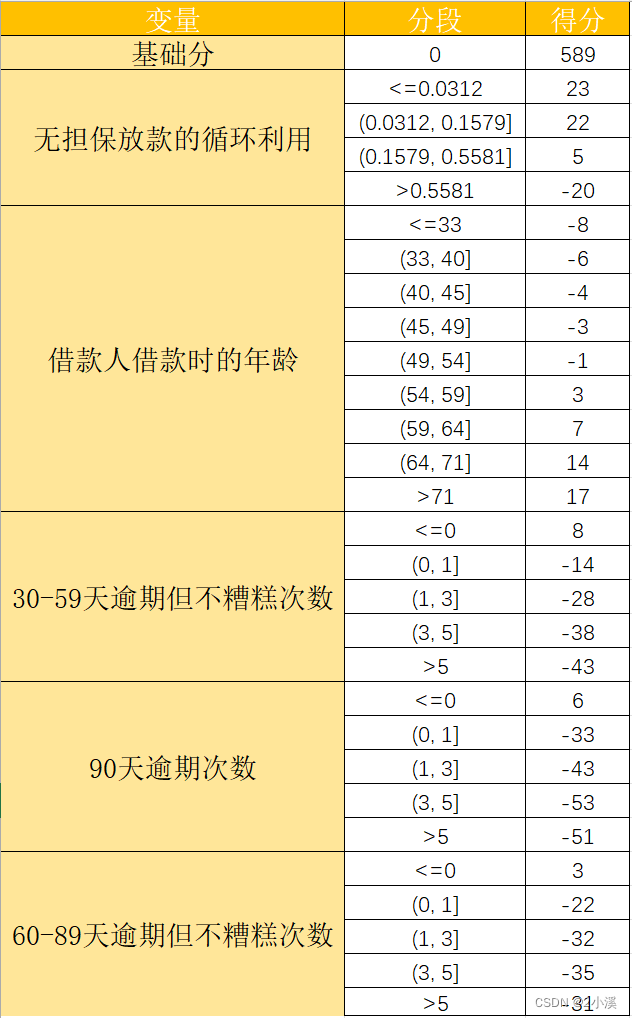
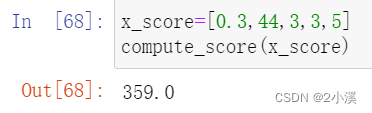
5.4 自动计算评分
建立一个函数,使得当输入x1,x2,x3,x7,x9的值时可以返回评分数
cut_t = [x1_cut,x2_cut,x3_cut,x7_cut,x9_cut]
# x为数组,包含x1,x2,x3,x7和x9的取值
def compute_score(x):
tot_score = baseScore
cut_d = copy.deepcopy(cut_t)
for j in range(len(cut_d)):
cut_d[j].append(x[j])
cut_d[j].sort()
for i in range(len(cut_d[j])):
if cut_d[j][i] == x[j]:
tot_score = score[j][i-1] +tot_score
return tot_score测试一下
基于python制作的信用评分卡就此完成!