文章目录
前言
gr-radar 中的 Static Target Simulator 模块用于在雷达系统中模拟静态目标。这种模拟在雷达信号处理、算法开发和系统验证中非常有用。通过模拟静态目标,可以测试雷达系统的目标检测、定位和追踪能力。这个模块允许用户设置多个目标的属性,如距离、速度、雷达截面等,从而生成对应的回波信号。下面对这个模块进行介绍并详细分析其底层 C++ 代码实现。
一、static Target simulator 简介

1、模块作用
Static Target Simulator 的主要作用是生成雷达回波信号,以模拟不同静态目标的存在。这对于验证和测试雷达系统的性能至关重要,特别是在缺乏实际目标或实验条件受限的情况下。通过调节不同的参数,用户可以模拟各种不同场景下的目标特性和环境噪声,进而评估雷达系统的响应和精度。
2、参数意义
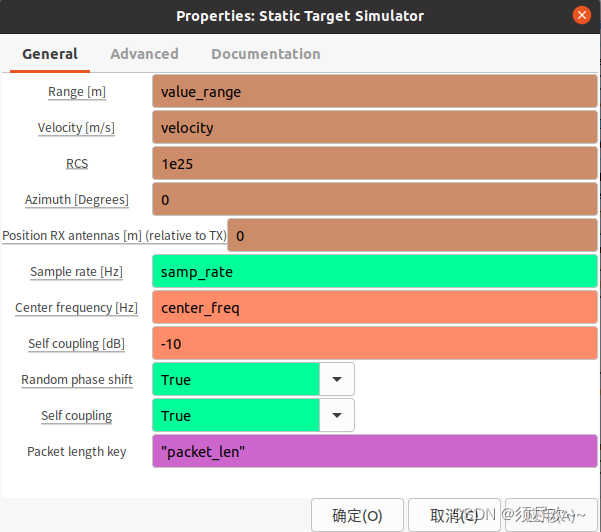
-
Range [m]:目标的距离,以米为单位。这个参数决定了目标相对于雷达的距离,从而影响回波信号的时间延迟。 -
Velocity [m/s]:目标的速度,以米/秒为单位。尽管是静态目标模拟器,这个参数可以设置为零或非零值,以模拟不同速度下的目标,主要用于测试系统对静态或缓慢移动目标的检测能力。 -
RCS:雷达截面(Radar Cross Section),一个表示目标反射能力的参数。数值越大,目标对雷达信号的反射越强。 -
Azimuth [Degrees]:标的方位角,以度为单位。方位角决定了目标相对于雷达的方向。 -
Position RX antennas [m] (relative to TX):接收天线相对于发射天线的位置,以米为单位。这个参数用于模拟不同接收位置的天线配置。 -
Sample rate [Hz]:采样率,以赫兹为单位。这个参数决定了信号处理的采样频率,是所有后续处理步骤的基准。 -
Center frequency [Hz]:雷达信号的中心频率,以赫兹为单位。这个参数决定了雷达发射信号的频率,也是多普勒效应计算的基础 -
Self coupling [dB]:自耦合,以分贝为单位。这个参数模拟雷达系统中发射和接收通道之间的耦合效应,影响接收到的信号强度。 -
Random phase shift:是否启用随机相位偏移。启用该选项可以模拟信号传播过程中引入的随机相位变化,增加模拟的现实性。 -
Self coupling:是否启用自耦合效应。启用该选项模拟接收信号中的自耦合噪声。 -
Packet length key:包长度键,用于定义数据包的长度。这对于数据流处理和同步非常重要。
二、C++ 具体实现
注释已标注清楚:
/* -*- c++ -*- */
/*
* Copyright 2014 Communications Engineering Lab, KIT.
*
* This is free software; you can redistribute it and/or modify
* it under the terms of the GNU General Public License as published by
* the Free Software Foundation; either version 3, or (at your option)
* any later version.
*
* This software is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
* GNU General Public License for more details.
*
* You should have received a copy of the GNU General Public License
* along with this software; see the file COPYING. If not, write to
* the Free Software Foundation, Inc., 51 Franklin Street,
* Boston, MA 02110-1301, USA.
*/
#ifdef HAVE_CONFIG_H
#include "config.h"
#endif
#include "static_target_simulator_cc_impl.h"
#include <gnuradio/io_signature.h>
#include <gnuradio/math.h>
#include <volk/volk.h>
namespace gr {
namespace radar {
namespace {
//! \f$ \sqrt{(4\pi)^3)}\f$
const double FOUR_PI_CUBED_SQRT = 44.54662397465366;
} // namespace
static_target_simulator_cc::sptr
static_target_simulator_cc::make(std::vector<float> range,
std::vector<float> velocity,
std::vector<float> rcs,
std::vector<float> azimuth,
std::vector<float> position_rx,
int samp_rate,
float center_freq,
float self_coupling_db,
bool rndm_phaseshift,
bool self_coupling,
const std::string& len_key)
{
return gnuradio::get_initial_sptr(
new static_target_simulator_cc_impl(range, // 距离
velocity, // 速度
rcs, // 雷达横截面积
azimuth, // 方位角
position_rx, // 接收位置
samp_rate, // 采样率
center_freq, // 雷达发射的信号频率
self_coupling_db, // 自耦合(可能是指天线间的耦合)的分贝值
rndm_phaseshift, // 是否使用随机相位偏移,这可能影响信号的相位特性
self_coupling, // 是否启用自耦合
len_key)); // 标识某种长度或关键数据的字符串
}
static_target_simulator_cc_impl::static_target_simulator_cc_impl(
std::vector<float> range,
std::vector<float> velocity,
std::vector<float> rcs,
std::vector<float> azimuth,
std::vector<float> position_rx,
int samp_rate,
float center_freq,
float self_coupling_db,
bool rndm_phaseshift,
bool self_coupling,
const std::string& len_key)
: gr::tagged_stream_block("static_target_simulator_cc", // 这是用于处理带有标签的流的块类型
gr::io_signature::make(1, 1, sizeof(gr_complex)),
gr::io_signature::make(position_rx.size(),
position_rx.size(),
sizeof(gr_complex)),
len_key)
{
setup_targets(range,
velocity,
rcs,
azimuth,
position_rx,
samp_rate,
center_freq,
self_coupling_db,
rndm_phaseshift,
self_coupling);
}
static_target_simulator_cc_impl::~static_target_simulator_cc_impl() {}
void static_target_simulator_cc_impl::setup_targets(std::vector<float> range,
std::vector<float> velocity,
std::vector<float> rcs,
std::vector<float> azimuth,
std::vector<float> position_rx,
int samp_rate,
float center_freq,
float self_coupling_db,
bool rndm_phaseshift,
bool self_coupling)
{
// 目标属性初始化
d_range = range;
d_velocity = velocity;
d_rcs = rcs;
d_azimuth = azimuth;
d_position_rx = position_rx;
d_center_freq =
center_freq; // center frequency of simulated hardware for doppler estimation
d_samp_rate = samp_rate;
d_hold_noutput = -1;
d_rndm_phaseshift = rndm_phaseshift;
d_self_coupling = self_coupling;
d_self_coupling_db = self_coupling_db;
// 标签和目标数量设置
// Setup rx_time tag
d_key = pmt::string_to_symbol("rx_time"); // 这里使用pmt库将字符串转换为符号,用于标记接收时间和源ID。这在处理流中的数据包时,可以帮助识别和追踪来自特定模拟器的数据。
d_srcid = pmt::string_to_symbol("stat_targ_sim");
// Get num targets
d_num_targets = // 通过获取range向量的大小来确定目标数量
range.size(); // FIXME: throw exceptions for len(range)!=len(velocity)!=...
// Get doppler frequencies
d_doppler.resize(d_num_targets);
d_filt_doppler.resize(d_num_targets);
// 计算多普勒频率:
for (int k = 0; k < d_num_targets; k++)
d_doppler[k] = 2 * d_velocity[k] * d_center_freq / c_light; // 使用经典的多普勒频率变化公式计算每个目标的多普勒频率
// Get timeshifts
d_timeshift.resize(d_num_targets);
d_timeshift_azimuth.resize(d_position_rx.size());
d_filt_time.resize(d_num_targets);
d_filt_time_azimuth.resize(d_position_rx.size());
// 这里计算了基于目标位置和方位的时移。这些计算帮助模拟信号传播时间,从而影响雷达接收信号的时间
for (int l = 0; l < d_position_rx.size(); l++) {
d_filt_time_azimuth[l].resize(d_num_targets);
d_timeshift_azimuth[l].resize(d_num_targets);
for (int k = 0; k < d_num_targets; k++) {
d_timeshift_azimuth[l][k] = // 估算了由于接收点与雷达的相对位置(考虑到方位角),信号在水平面上的投影距离
d_position_rx[l] * std::sin(d_azimuth[k] * GR_M_PI / 180.0); // 雷达接收器的位置 * sin(第k个目标的方位角 * 3.14 / 180)
}
}
for (int k = 0; k < d_num_targets; k++)
d_timeshift[k] = 2.0 * d_range[k] / c_light; // 时延
// Get signal amplitude of reflection with free space path loss and rcs (radar
// equation)
// 反射信号幅度计算
d_scale_ampl.resize(d_num_targets);
for (int k = 0; k < d_num_targets; k++) {
// Factor out all terms out of the sqrt except the RCS:
// 根据雷达方程计算信号反射幅度
d_scale_ampl[k] = c_light * std::sqrt(d_rcs[k]) / FOUR_PI_CUBED_SQRT /
(d_range[k] * d_range[k]) / d_center_freq;
}
// 如果启用了随机相位偏移,这段代码设置了随机数种子并为每个目标预备相位偏移的数据结构。
// 随机相位偏移可以模拟信号传输过程中的不确定性和噪声。
if (d_rndm_phaseshift) {
// Resize phase shift filter
d_filt_phase.resize(d_num_targets);
// Setup random numbers
std::srand(std::time(NULL)); // initial with time
}
}
int static_target_simulator_cc_impl::calculate_output_stream_length(
const gr_vector_int& ninput_items)
{
int noutput_items = ninput_items[0];
return noutput_items;
}
int static_target_simulator_cc_impl::work(int noutput_items,
gr_vector_int& ninput_items,
gr_vector_const_void_star& input_items,
gr_vector_void_star& output_items)
{
const gr_complex* in = (const gr_complex*)input_items[0]; // 这个数组代表输入信号
gr_complex* out;
// Set output items to tagged stream length
noutput_items = ninput_items[0]; // 将输出项目数设置为与第一个输入信号的项目数相同,确保输入输出同步
// Check if new filter, buffer or fft plan is necessary
// 检查和设置FFT计划
// 如果当前输出项目数与前一次不同,则需要重新设置FFT和IFFT计划,调整频率向量和相关缓冲区。
// 这是因为FFT的性能和精度依赖于数据长度和样本数。
if (d_hold_noutput != noutput_items) {
// Set length buffer in loop
d_hold_in.resize(noutput_items);
// Setup fft and ifft
// 虽然创建了FFT和IFFT的计划,这并不意味着它们立即连续执行而没有任何实际效果。
// 相反,这种做法是为了效率和灵活性:预先定义如何进行这些变换,然后在实际需要时高效地执行。
d_in_fft.resize(noutput_items);
d_fft_plan = fftwf_plan_dft_1d(noutput_items, // 进行傅里叶变换的数据点的数量
reinterpret_cast<fftwf_complex*>(&d_hold_in[0]), // 指向你想要变换的数据
reinterpret_cast<fftwf_complex*>(&d_in_fft[0]), // 接收变换的结果
FFTW_FORWARD, // 正向傅里叶变换
FFTW_ESTIMATE); // 它指示FFTW库在创建计划时不进行任何实际的数据变换
d_ifft_plan = fftwf_plan_dft_1d(noutput_items,
reinterpret_cast<fftwf_complex*>(&d_in_fft[0]),
reinterpret_cast<fftwf_complex*>(&d_hold_in[0]),
FFTW_BACKWARD,
FFTW_ESTIMATE);
// Setup frequency vector for shift in frequency domain
// 频率向量设置
d_freq.resize(noutput_items);
// 计算并设置频率向量,用于后续的频域处理。这里根据采样率和输出项目数计算每个频点的实际频率值。
for (int i = 0; i < noutput_items; i++) {
if (i < noutput_items / 2) // 这部分包含了从0到正的最大频率(不包括奈奎斯特频率)的频率分量。它们是正频率,从0增加到采样频率的一半
d_freq[i] =
i * (float)d_samp_rate / (float)noutput_items; // zero to samp_rate/2
else // 这部分包含了从负的最大频率到接近0的负频率的频率分量。因为数字FFT的对称性,这部分的频率实际上是“包装”或“折回”到负频率去的。
d_freq[i] = i * (float)d_samp_rate / (float)noutput_items -
(float)d_samp_rate; // -samp_rate/2 to zero
}
// Setup freq and time shift filter, resize phase shift filter
// 负责设置和计算用于模拟多普勒效应、时间延迟和相位偏移的滤波器,是雷达信号处理中常见的操作
// 循环初始化每个目标的滤波器:
for (int k = 0; k < d_num_targets; k++) {
// 多普勒滤波器和随机相位滤波器的初始化, 每个滤波器大小与输出项数相等
d_filt_doppler[k].resize(noutput_items);
if (d_rndm_phaseshift)
d_filt_phase[k].resize(noutput_items);
// 计算多普勒滤波器
d_phase_doppler = 0;
for (int i = 0; i < noutput_items; i++) {
// Doppler shift filter and rescaling amplitude with rcs
// 应用雷达截面(RCS)标度:d_scale_ampl[k]是根据目标的雷达截面计算的标度因子,用于调整反射信号的强度
d_filt_doppler[k][i] = std::exp(d_phase_doppler) * d_scale_ampl[k];
// 多普勒滤波器的计算:基于每个目标的多普勒频移值d_doppler[k],这个值通过模拟目标的相对速度计算得到。每个频点的相位增量由目标的速度和采样率决定。相位被模的2 * GR_M_PI以保持在合理范围内。
d_phase_doppler =
gr_complex(0, std::fmod(std::imag(d_phase_doppler) +
2 * GR_M_PI * d_doppler[k] / (float)d_samp_rate,
2 * GR_M_PI)); // integrate phase (with plus!)
}
// 计算时间延迟滤波器
d_filt_time[k].resize(noutput_items);
d_phase_time = 0;
for (int i = 0; i < noutput_items; i++) {
// Time shift filter, uses target range
// 时间延迟滤波器的计算:利用目标的时间延迟d_timeshift[k]和每个频率点d_freq[i]计算相位
d_phase_time =
gr_complex(0, std::fmod(2 * GR_M_PI * (d_timeshift[k]) // range time shift
* d_freq[i],
2 * GR_M_PI)); // integrate phase (with minus!)
// 幅度校正:除以noutput_items是为了在执行FFT和IFFT后校正幅度,这是因为FFT和IFFT的缩放不同
// 计算了一个时间延迟滤波器,并对其进行了归一化,以便在FFT和IFFT之后正确地调整幅度
d_filt_time[k][i] =
std::exp(-d_phase_time) /
(float)noutput_items; // div with noutput_item to correct amplitude
// after fft->ifft
}
// 结合方位和接收位置的时间延迟滤波器
// 此部分进一步考虑了目标的方位角和接收位置对时间延迟的影响。
for (int l = 0; l < d_position_rx.size();
l++) { // Do time shift filter with azimuth and position, there are two
// time shift filters to avoid problems with significant digits of
// float
d_filt_time_azimuth[l][k].resize(noutput_items);
d_phase_time = 0;
for (int i = 0; i < noutput_items; i++) {
// Time shift filter, uses azimuth and RX position
d_phase_time =
gr_complex(0, std::fmod(2 * GR_M_PI *
(d_timeshift_azimuth[l][k]) // azimuth time shift
* d_freq[i],
2 * GR_M_PI)); // integrate phase (with minus!)
// 计算了一个关于方位角和接收位置的时间延迟影响的滤波器
d_filt_time_azimuth[l][k][i] =
std::exp(-d_phase_time); // do not div with noutput_items, is done
// with range timeshift filter
}
}
}
// Resize hold of noutput_items
// 更新或存储当前处理的输出项的数量
d_hold_noutput = noutput_items;
}
// Setup random phase shift
// 用来为雷达信号处理中的每个目标添加随机相位偏移的。随机相位偏移是在雷达和其他通信系统中用于模拟环境噪声或信号多路径效应的一种技术
if (d_rndm_phaseshift) {
gr_complex phase_random_hold; // 用来临时存储计算出的随机相位值
for (int k = 0; k < d_num_targets; k++) { // 系统需要为每个目标单独设置随机相位偏移
// 这行代码生成一个随机相位值,范围从0到2π,std::rand() % 1000生成一个0到999的随机整数,
// +1使得范围变为1到1000,除以1000.0将其标准化到0.001到1.0,乘以2π将这个比例转换为一个
// 完整的圆周范围的角度
// gr_complex(0, ...)构造一个复数,其实部为0,虚部为计算出的角度,表示在复平面上的纯相位偏移。
phase_random_hold = gr_complex(0, 2 * GR_M_PI * float((std::rand() % 1000 + 1) / 1000.0));
// 使用欧拉公式e^{jθ}将角度转换为复数形式的相位因子。这里的相位因子用于后续的信号处理中,对信号进行相位旋转
d_phase_random = std::exp(phase_random_hold);
std::fill_n(&d_filt_phase[k][0], noutput_items, d_phase_random);
}
}
// Go through RXs
// 负责处理接收到的信号,应用多普勒偏移、时间延迟、相位偏移,并将结果写入输出缓冲区
for (int l = 0; l < d_position_rx.size(); l++) { // 遍历所有的接收器位置
// Setup pointer on output buffer
out = (gr_complex*)output_items[l]; // 每个接收器设置一个指向输出缓冲区的指针
// Set rx_time tag
// 设置接收时间标签:
// 这几行代码计算接收时间并创建一个时间戳,将其作为标签添加到输出流中
d_time_sec = nitems_written(l) / d_samp_rate;
d_time_frac_sec = nitems_written(l) / (float)d_samp_rate - d_time_sec;
d_val = pmt::make_tuple(
pmt::from_uint64(d_time_sec),
pmt::from_double(d_time_frac_sec)); // FIXME: correct implementation?
add_item_tag(l, nitems_written(l), d_key, d_val, d_srcid);
// Set output to zero
// 这行代码将输出数组初始化为零,为即将到来的数据处理做准备
std::memset(out, 0, noutput_items * sizeof(gr_complex));
// Go through targets and apply filters
// 处理每个目标的信号
for (int k = 0; k < d_num_targets; k++) {
// 这些行代码首先将输入信号与多普勒滤波器相乘,然后执行FFT将信号转到频率域,应用时间延迟滤波器,
// 最后通过IFFT返回到时域。这些操作模拟信号如何受到目标移动和位置变化的影响
// Add doppler shift
volk_32fc_x2_multiply_32fc(
&d_hold_in[0],
in,
&d_filt_doppler[k][0],
noutput_items); // add doppler shift with rescaled amplitude
// Add time shift
fftwf_execute(d_fft_plan); // go to freq domain
volk_32fc_x2_multiply_32fc(&d_in_fft[0],
&d_in_fft[0],
&d_filt_time[k][0],
noutput_items); // add timeshift with multiply
// exp-func in freq domain (range)
volk_32fc_x2_multiply_32fc(
&d_in_fft[0],
&d_in_fft[0],
&d_filt_time_azimuth[l][k][0],
noutput_items); // add timeshift with multiply exp-func in freq domain (rx
// position with azimuth and range)
fftwf_execute(d_ifft_plan); // back in time domain
// 应用随机相位偏移
if (d_rndm_phaseshift) {
// Add random phase shift
volk_32fc_x2_multiply_32fc(&d_hold_in[0],
&d_hold_in[0],
&d_filt_phase[k][0],
noutput_items); // add random phase shift
}
// Add to output
// 累加处理后的信号到输出
for (int i = 0; i < noutput_items; i++)
out[i] += d_hold_in[i];
}
// Add self coupling
// 如果启用,添加自耦合
// 这部分代码在信号中添加自耦合效应,模拟接收器自身的干扰。这是一种常见的模拟实际接收条件的方法
if (d_self_coupling) {
for (int i = 0; i < noutput_items; i++)
out[i] += (gr_complex)pow(10, d_self_coupling_db / 20.0) *
in[i]; // d_self_coupling_db gives scaling of power
}
}
// Tell runtime system how many output items we produced.
return noutput_items;
}
} /* namespace radar */
} /* namespace gr */
三、核心公式
1、多普勒
d_doppler[k] = 2 * d_velocity[k] * d_center_freq / c_light;
这里的公式可以写成数学表达式如下:
f
d
=
2
v
λ
f_d=\frac{2v}{\lambda}
fd=λ2v
λ
=
c
f
\lambda=\frac{c}{f}
λ=fc
2、接收点与雷达的相对位置
d_timeshift_azimuth[l][k] = // 估算了由于接收点与雷达的相对位置(考虑到方位角),信号在水平面上的投影距离
d_position_rx[l] * std::sin(d_azimuth[k] * GR_M_PI / 180.0); // 雷达接收器的位置 * sin(第k个目标的方位角 * 3.14 / 180)
这里的公式可以写成数学表达式如下:
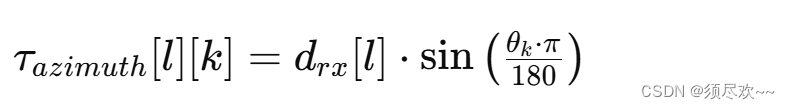
其中:

代码中的计算过程:

3、时间延迟
d_timeshift[k] = 2.0 * d_range[k] / c_light;
这个公式的数学表达式为:

其中:

4、根据雷达方程计算信号反射幅度
d_scale_ampl[k] = c_light * std::sqrt(d_rcs[k]) / FOUR_PI_CUBED_SQRT /
(d_range[k] * d_range[k]) / d_center_freq;
这个公式的数学表达式为:

其中:

代码中的计算过程:

5、多普勒滤波器
d_phase_doppler = gr_complex(0, std::fmod(std::imag(d_phase_doppler) +
2 * GR_M_PI * d_doppler[k] / (float)d_samp_rate,
2 * GR_M_PI));
这里的公式可以写成数学表达式如下:
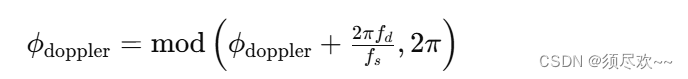
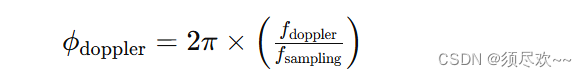
其中:

代码中的计算过程:
①、累积相位偏移:
std::fmod(std::imag(d_phase_doppler) + 2 * GR_M_PI * d_doppler[k] / (float)d_samp_rate, 2 * GR_M_PI)

②、更新相位偏移:
d_phase_doppler = gr_complex(0, std::fmod(...));
将新的相位偏移值存储在 d_phase_doppler 中,实部为0,虚部为计算出的相位偏移值。
6、多普勒相位偏移
d_phase_time = gr_complex(0, std::fmod(2 * GR_M_PI * (d_timeshift[k]) // range time shift * d_freq[i], 2 * GR_M_PI));
这里的数学表达式可以写为:
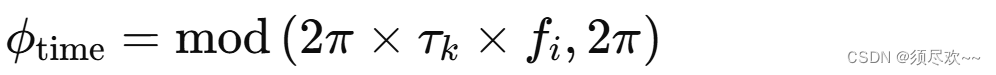
其中:

代码中的计算过程

7、时间延迟滤波器
d_filt_time[k][i] =
std::exp(-d_phase_time) /
(float)noutput_items; // div with noutput_item to correct amplitude
这个表达式可以写成数学形式如下:
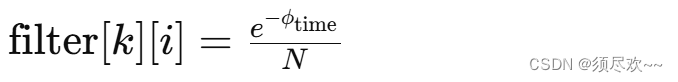
其中:

代码中的计算过程:

8、目标的方位角和接收位置对时间延迟的影响
d_phase_time = gr_complex(0, std::fmod(2 * GR_M_PI *
(d_timeshift_azimuth[l][k]) // azimuth time shift
* d_freq[i],
2 * GR_M_PI));
这里的数学表达式可以表示为:
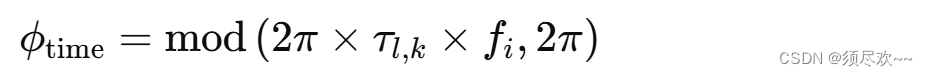
其中:

代码中的计算过程:

9、方位角和接收位置的时间延迟影响的滤波器
d_filt_time_azimuth[l][k][i] = std::exp(-d_phase_time);
数学表达式可以写为:
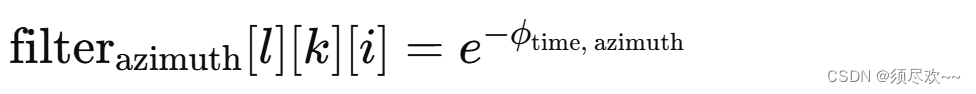
其中:

代码中的计算过程:

我的qq:2442391036,欢迎交流!