前言
学习笔记,仅供学习,不做商用,如有侵权,联系我删除即可
目标
- 理解针孔相机的模型、内参与径向畸变参数。
- 理解一个空间点是如何投影到相机成像平面的。
- 掌握OpenCV的图像存储与表达方式。
- 学会基本的摄像头标定方法。
一、相机模型
1.1 针孔相机模型
针孔相机模型如下图所示:
O':主点

根据针孔相机模型和相似三角形原理,有:关系。为了消除负号,把像面翻转导共轭面位置即可获得:
,整理得
。
成像平面到像素坐标:,(cx,cy)主点坐标,(dx,dy):像元尺寸。矩阵形式如下:
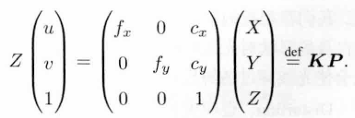
Z:深度,相机坐标系下三维空间点距离光心的距离。
K:内参矩阵。
世界坐标 --> 相机坐标 --> (投影成像) 归一化平面 --> 像素坐标系

T:变换矩阵
1.2 畸变模型
径向畸变:由透镜形状引起的畸变
- 桶形畸变
- 枕型畸变
切向畸变:组装时透镜和成像面不是严格平行引入的畸变。

畸变矫正模型:

畸变矫正的流程:

相机标定常用张正友标定法。
当使用Matlab或Opencv进行标定时,畸变系数的排列顺序:(k1,k2,p1,p2,k3)
单目相机成像过程总结:

1.3 双目相机模型
双目相机成像原理:

根据上图的几何关系,有以下关系: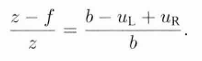
整理后可得: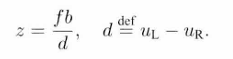 d:视差(disparity),同一点在左右相机相面横坐标之差。
d:视差(disparity),同一点在左右相机相面横坐标之差。
d最小为一个像素,所以双目相机模型的深度z具有最大值:fb
1.4 RGB-D相机模型
不需要计算深度,主动测量深度,按实现原理可分为两类:
- 结构光(Structured Light)
- 飞行时间法(Time-of-Flight, ToF)
二、图像