机器人--矩阵运算

2024-06-07 18:22
算法, 机器人
121人已看

两个矩阵相乘的含义

P点在坐标系B中的坐标系PB，需要乘以B到A到变换矩阵TAB。

M点在B坐标系中的位姿MB，怎么计算M在A中的坐标系？

矩阵左乘和矩阵右乘

左乘和右乘的含义

逆矩阵

逆矩阵求解

链接

四元素的逆矩阵

实部不变，虚部求反。

A=[w,Qx,Qy,Qz]的逆矩阵：A-1=[W,-Qx,-Qy,-Qz];

验证：

逆矩阵的意义

一个矩阵*另一个矩阵的逆矩阵

一个点在坐标系中的位置用X表示，姿态用Q表示。

有两个点1，2，位姿分别是：X1，Q1，X2,Q2，

不管是欧拉角还是四元素，都是描述姿态的。

点坐标系的意义
机器人中，一个有坐标轴的点就是一个坐标系。

任何点相对于世界坐标系的位姿(位置+姿态)就是这个点所代表的坐标系的变换矩阵(位置矩阵+旋转矩阵)。

变换矩阵*位置矢量

    double tool_xyz[3];
    simGetObjectPosition(tool_handle, sim_handle_world, tool_xyz);

    C3Vector tr(0, 0, z/2.0);
    //工具的位置矢量
    C7Vector tool_tr(C3Vector(MetricNumber<EUnit::m>(tool_xyz[0]).toMillimeter(),
                              MetricNumber<EUnit::m>(tool_xyz[1]).toMillimeter(),
                              MetricNumber<EUnit::m>(tool_xyz[2]).toMillimeter()));
    C3Vector result = tool_tr * tr;  //工具包络在世界坐标系下的位置矢量
    LOG_F(kInfo,"tool x===={}",tool_xyz[0]);
    LOG_F(kInfo,"tool y===={}",tool_xyz[1]);
    LOG_F(kInfo,"tool z===={}",tool_xyz[2]);
    LOG_F(kInfo,"tool envelope x===={}",result.data[0]);
    LOG_F(kInfo,"tool envelope y===={}",result.data[1]);
    LOG_F(kInfo,"tool envelope z===={}",result.data[2]);

输出：

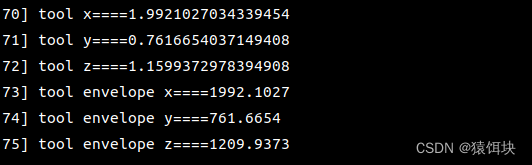
tool_tr是工具相对于世界坐标系的位姿；

计算出来的结果位于工具坐标系的上方，也就是tr