【Python实战因果推断】10

【Python实战因果推断】10_元学习器5

Double-ML for CATE estimation

Visual intuition for Double-ML

Tree-Based Learners and Neural Net Learners

Key Ideas

Double-ML for CATE estimation

要从 Double-ML 模型中获得 CATE 预测，您需要做一些调整。从根本上说，您需要允许因果参数 $\tau$ 根据单元的协变量变化而变化。

$Y_i=\hat{\mu}_y\big(X_i\big)+\tau\big(X_i\big)\big(T_i-\hat{\mu}_t(X)\big)+\hat{\epsilon}_i$

其中， $\hat{\mu}_{y}$ 和 $\hat{\mu}_{t}$ 分别是根据特征 X 预测干预结果和治疗方法的模型。如果重新排列项，就可以隔离误差：

$\hat{\epsilon}_i=\Big(Y_i-\hat{\mu}_y(X_i)\Big)-\tau\big(X_i\big)\big(T_i-\hat{\mu}_t(X)\big)$

这简直棒极了，因为现在你可以称其为因果损失函数了。这意味着，如果你最小化这个损失的平方，你就能估算出 τ 的期望值，这就是你想要的 CATE：

$\hat{L}_n(\tau(x))=\frac{1}{n}\sum\limits_{i = 1}^n\left(\left(Y_i-\widehat{M}_y(X_i)\right)-\tau(X_i)\left(T_i-\widehat{M}_t(X)\right)\right)^2$

这种损失也被称为 R 损失，因为它是 R 学习器最小化的损失。那么，如何最小化这个损失函数呢？其实有多种方法，但在这里你会看到最简单的一种。首先，为了简化技术符号，让我们用干预和结果的残差重写损失函数：

$\hat{L}_n(\tau(x))=\frac{1}{n}\Sigma_{i=1}^n\left(\tilde{Y}_i-\tau(X_i)\tilde{T}_i\right)^2$

最后，你可以用代数方法将 $\tilde{T}_{i}$ 从括号中取出，并将 $\tau(X_{i})$ 从损失函数的平方部分中分离出来：

$\hat{L}_{n}(\tau(x))=\frac{1}{n}\sum_{i=1}^{n}\tilde{T}_{i}^{2}\biggl(\frac{\tilde{Y}_{i}}{\tilde{T}_{i}}-\tau\bigl(X_{i}\bigr)\biggr)^{2}$

最小化前面的损失相当于最小化括号内的内容，但每个项的权重都是 $\tilde{T}_{i}^{2}$ 。任何预测性 ML 模型都能做到这一点。

但是，等一下！你已经看到了！这就是你用来计算均方误差的转换目标！的确如此。然后，我让你们相信再说一遍，编码非常简单：

 y_star = y_res/t_res
 w = t_res**2
 cate_model = LGBMRegressor().fit(train[X], y_star, sample_weight=w)
 test_r_learner_pred = test.assign(cate = cate_model.predict(test[X]))

我非常喜欢这个学习器的一点是，它可以直接输出 CATE 估计值。无需使用 S 学习器时的所有额外步骤。此外，从下面的图中可以看出，它在 CATE 排序方面做得相当不错，这是以累积增益来衡量的：

在这个例子中，Double/Debiased-ML 的性能与 Slearner 非常相似。这 可能是因为干预足够强，所以 S-learner 中的 ML 模型对其赋予了很高的重要性。另外，干预是随机的，这意味着 Double-ML 中的μt 模型并没有真正发挥作用。因此，为了更好地了解 Double-ML 的真正威力，让我们来看一个更能说明问题的例子。

Visual intuition for Double-ML

请看下面的模拟数据。其中有两个协变量： $x_{c}$ 是混杂因素， $x_{h}$ 不是。另外， $x_{h}$ 会导致效应异质性。 $x_{h}$ 只有三个值： 1、2 和 3。另外，由于 $x_{h}$ 是均匀分布的，因此 ATE 只是 CATE 的简单平均值，即 3。最后，请注意混杂因素 $x_{c}$ 对干预和治疗效果的非线性影响：

 np.random.seed(123)
 n = 5000
 x_h = np.random.randint(1, 4, n)
 x_c = np.random.uniform(-1, 1, n)
 t = np.random.normal(10 + 1*x_c + 3*x_c**2 + x_c**3, 0.3)
 y = np.random.normal(t + x_h*t - 5*x_c - x_c**2 - x_c**3, 0.3)
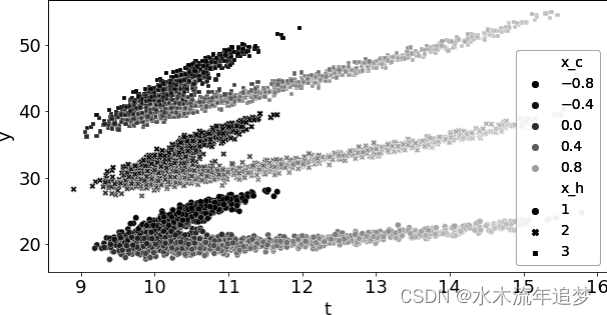
 df_sim = pd.DataFrame(dict(x_h=x_h, x_c=x_c, t=t, y=y))

下面是该数据的曲线图。每一团点都是由 $x_{h}$ 定义的一组。颜色编码代表混杂因素 $x_{c}$ 的值。请注意其中的非线性形状：

现在，让我们看看 Double-ML 是如何处理这些数据的。首先，让我们得到残差 T 和 Y。由于这里的数据并不多，所以请限制您的 ML 模型，使其具有 max_depth=3 的树。我在去偏模型中只包含 $x_{c}$ ，因为这是唯一的混杂因素。去噪模型包含了两个协变量，因为这两个协变量都会导致结果，包含它们会减少噪音：

 debias_m = LGBMRegressor(max_depth=3)
 denoise_m = LGBMRegressor(max_depth=3)
 t_res = cross_val_predict(debias_m, df_sim[["x_c"]], df_sim["t"],
 cv=10)
 y_res = cross_val_predict(denoise_m, df_sim[["x_c", "x_h"]],df_sim["y"],
 cv=10)
 df_res = df_sim.assign(
 t_res = df_sim["t"] - t_res,
 y_res = df_sim["y"] - y_res
 )

一旦有了这些残差， $x_{c}$ 引起的混杂偏差就应该消失了。尽管它是非线性的，但我们的 ML 模型应该能够捕捉到这种非线性，并消除所有偏差。因此，如果对 Y 对 T 进行简单回归，就能得到正确的 ATE：

 import statsmodels.formula.api as smf
 smf.ols("y_res~t_res", data=df_res).fit().params["t_res"]
 
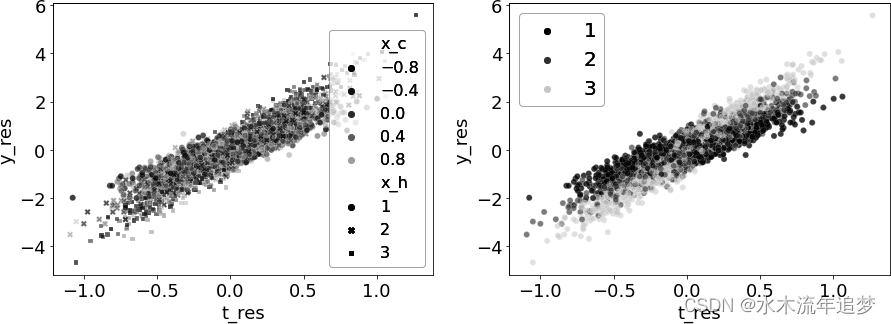
 3.045230146006292

接下来，让我们关注 CATE 估计。下图左侧的图显示了残差之间的关系，并根据混杂因素 xc 对每个点进行了颜色编码。请注意，该图的颜色没有规律可循。这表明 $x_{c}$ 造成的混杂因素已全部去除。数据看起来就像是随机分配的干预。

下一幅图通过 $x_{h}$ （即干预治疗异质性的特征）对相同的关系进行了颜色编码。最深的点（ $x_{h}$ = 1）似乎对干预不那么敏感，如较低的斜率所示。相比之下，浅色的点（ $x_{h}$ = 3）似乎对干预更敏感。观察这幅图，您能想到提取这些敏感性的方法吗？要回答这个问题，请注意两个残差都以零为中心。这意味着，决定 xh 所定义的所有组斜率的直线都应交零。现在，请回忆一下，一条直线的斜率可以根据两点估算为 Δy/Δt。但是，由于这条直线的截距应为零，因此简化为 y/t。因此，你可以将 Double-ML 的 Y* 目标视为经过该点且截距为零的直线的斜率。

但有一个问题。T 和 Y 的平均值都接近于零。你知道当你除以一个接近零的数字时会发生什么？没错，它会非常不稳定，产生大量的噪声。这就是权重 T 发挥作用的地方。通过赋予 T 值高的点更多的重要性，你基本上就把注意力集中在了方差较小的区域。

 df_star = df_res.assign(
 y_star = df_res["y_res"]/df_res["t_res"],
 weight = df_res["t_res"]**2,
 )
 for x in range(1, 4):
 cate = np.average(df_star.query(f"x_h=={x}")["y_star"],
 weights=df_star.query(f"x_h=={x}")["weight"])
 
 print(f"CATE x_h={x}", cate)
 
 CATE x_h=1 2.019759619990067
 CATE x_h=2 2.974967932350952
 CATE x_h=3 3.9962382855476957

您也可以从 Y* 与 T 的关系图中看出我在说什么。在这里，我再次按 xh 进行了颜色编码，但现在我添加了等于 T 的权重：

我喜欢这幅图，因为它清楚地显示了权重的作用。当你接近图的中心时，Y* 的方差会增加很多。因为我限制了 Y 轴的范围，所以你看不到，但实际上有一些点一直延伸到 2000 和 2000！幸运的是，这些点都接近 T = 0，所以它们的权重很小。现在，你对 DoubleML 有了更直观的认识。

Tree-Based Learners and Neural Net Learners

本章并不打算详尽列举目前所有的元学习工具。我只列出了我个人认为最有用的元学习器。不过，除了这里介绍的四种学习器之外，还有其他一些学习器值得一提。

首先，苏珊-阿特伊（Susan Athey）和斯特凡-瓦格（Stefan Wager）使用修正决策树在效应异质性方面做了大量开创性工作。你可以在ecml和causalml等因果推理库中找到基于树的CATE学习器。

Key Ideas

本章扩展了学习组水平治疗效果 τ 的思路。你学到了如何重新利用通用机器学习模型进行条件平均治疗效果（CATE）估计，而不是仅仅在回归模型中将治疗变量与协变量 X 交互作用，即所谓的元学习器。具体来说，您了解了四种元学习器，其中两种只适用于分类干预，另外两种适用于任何类型的干预。

首先，T-learner 拟合一个机器学习模型来预测每种治疗 T 的 Y，然后，得出的干预结果模型 μt 可用来估计治疗效果。例如，在二元干预的情况下：

$\hat{\tau}(X_i)=\widehat{\mu_1}(X_i)-\widehat{\mu_0}(X_i)$

如果所有干预水平的观测数据都很多，T-learner 的效果就会很好。否则，在小数据集中估计的模型可能会出现正则化偏差。您看到的下一个学习器 X 学习器试图通过使用倾向得分模型来降低在小样本上训练的任何 μt 的重要性，从而解决这个问题。

为了处理连续干预，你们学习了 S-学习器，它只需估计 $E[Y|T,X]$ 。也就是说，它预测的是将干预作为特征之一的结果。该模型可用于在给定处理值网格的情况下对 Yt 进行反事实预测。这样就得到了一个特定单位的粗略干预反应函数，之后需要将其归纳为一个单一的斜率参数。

最后，但并非最不重要的一点，你们了解了双 ML。其思路是使用通用 ML 模型和折外预测，分别得到治疗和干预结果残差 $T-E[T|X]$ 和 $Y-E[Y|X]$ 。这可以理解为 FWL 正交化的改进版。一旦得到了这些残差--称之为 $\tilde{T}$ 和 $\tilde{Y}$ --就可以构建一个近似 $\tau(x_{i})$ 的目标： $Y^\star=\tilde{Y}/\tilde{T}$

在使用权重 $\tilde{T}^2$ 的同时，使用任何 ML 模型预测该目标，都会产生一个可以直接输出 CATE 预测结果的 ML 模型。

最后，值得记住的是，所有这些方法都依赖于无边界假设。不管您试图用于 CATE 估计的算法听起来有多炫，要想让它们消除偏差，您的数据中必须包含所有相关的混杂因素。具体来说，无混杂性允许您将条件期望值的变化率解释为治疗反应函数的斜率：

$\frac{\partial}{\partial t}E[Y(t)|X]=\frac{\partial}{\partial t}E[Y|T=t,X]$