个人技术分享

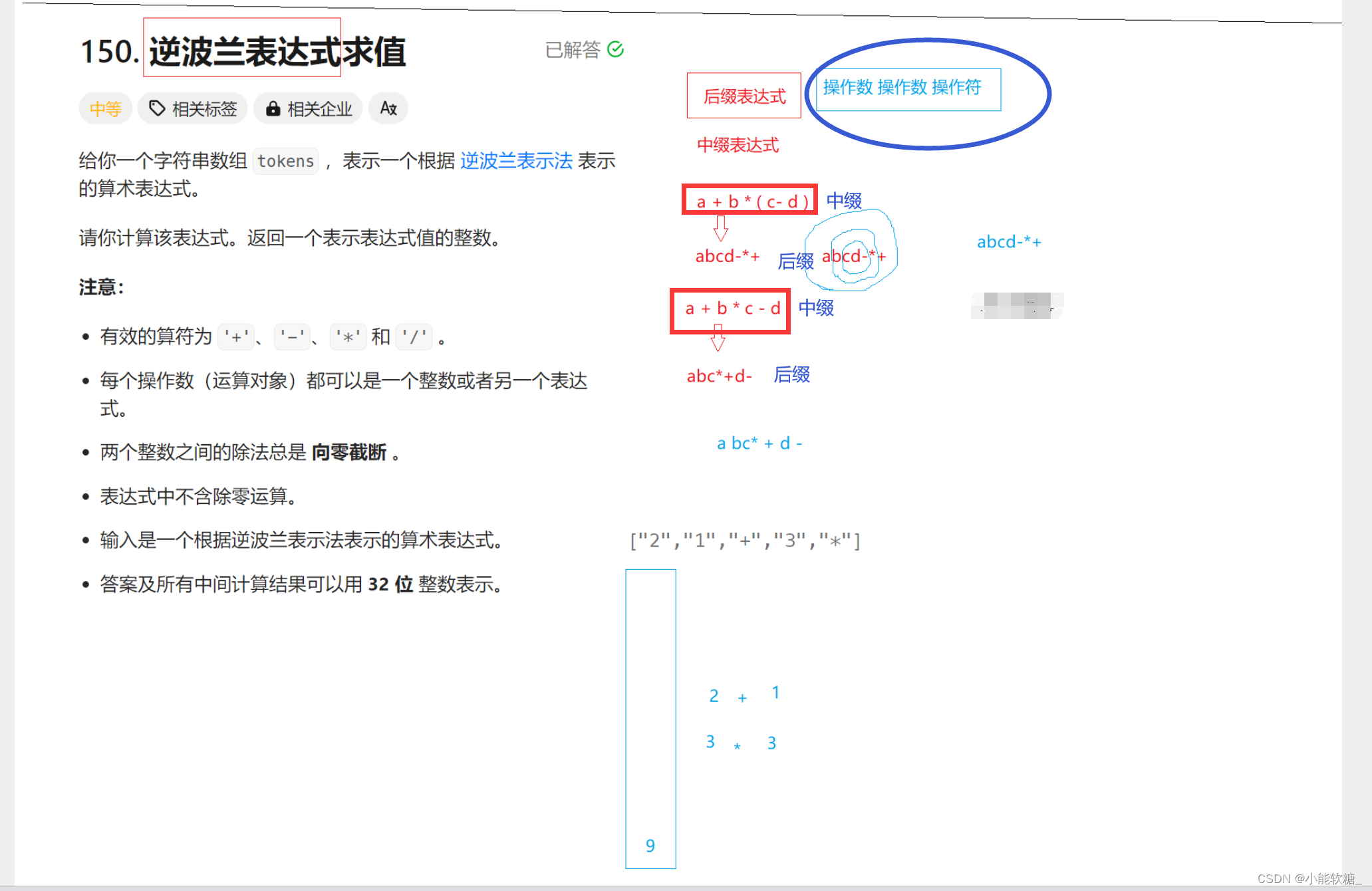
一、题目描述：

什么是逆波兰表达式？逆波兰表达式就是后置计算！

二、算法原理：

（1）平时用的表达式都是中缀表达式，根据栈的性质，表达式中，会有以下两种情况：

    ①当遇到操作数时就入栈

    ②当遇到操作符就把栈顶数据拿出来和操作符后面的数据进行运算，运算结果再入栈

（2）但是中缀转后缀表达式和中缀表达式不同的就是调整运算符的优先级

    如果是操作数，直接入栈

    如果是操作符，从栈里连续取出两个操作数进行计算，并将结果入栈

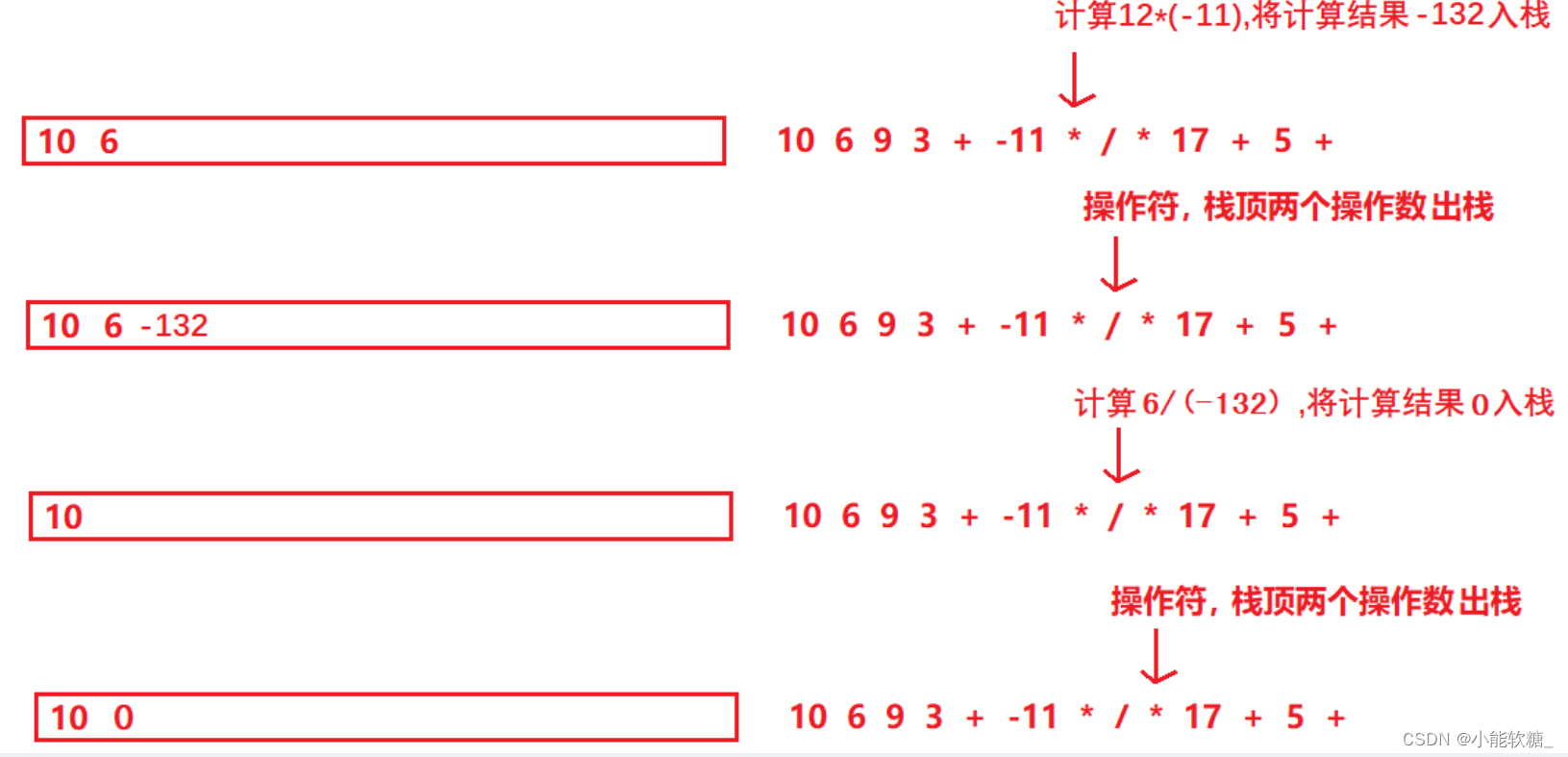
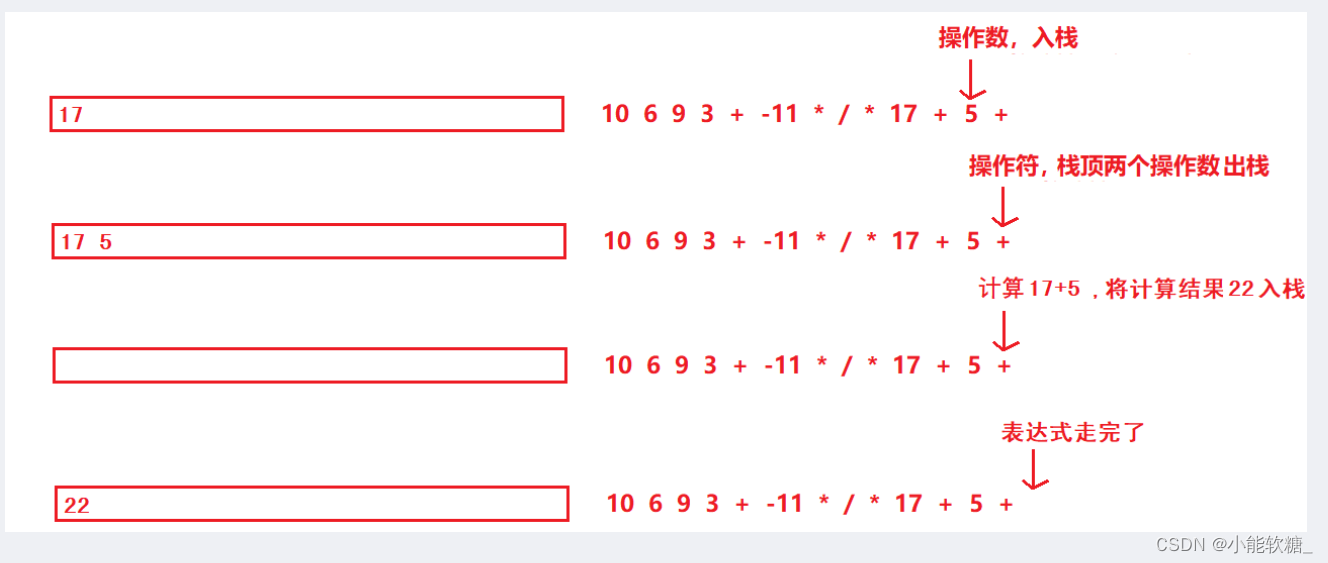
（3）代码给定的入参是vector不是string，因为不知道一个操作数有几个项，得用特殊符号比如空格去分割，而示例每项都是一个字符串，vector的类型是string就更方便获取表达式的每一个元素

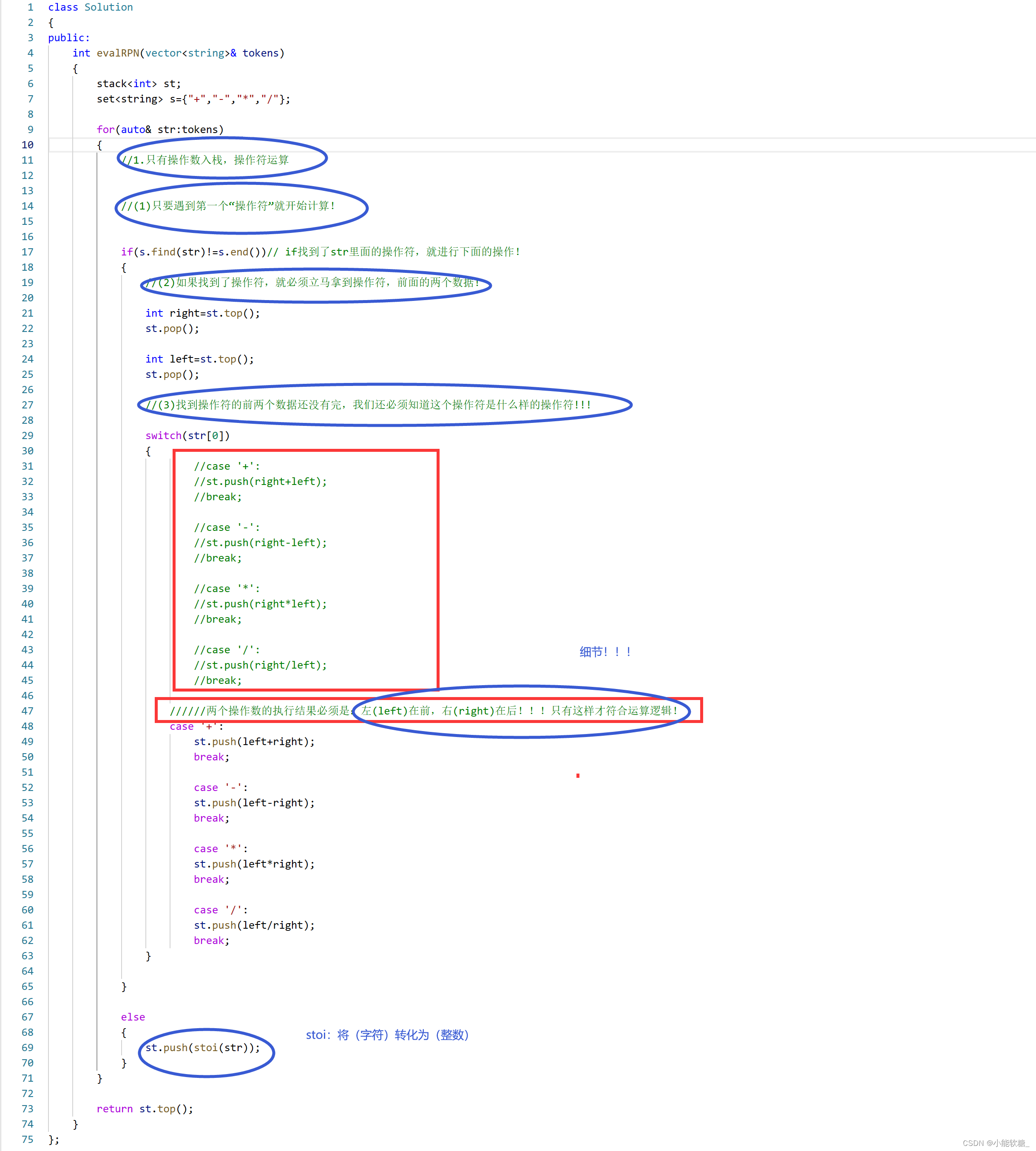
三、代码实现：

class Solution 
{
public:
    int evalRPN(vector<string>& tokens) 
    {
        stack<int> st;
        set<string> s={"+","-","*","/"};

        for(auto& str:tokens)
        {
            //1.只有操作数入栈，操作符运算


            //(1)只要遇到第一个“操作符”就开始计算！


            if(s.find(str)!=s.end())// if找到了str里面的操作符，就进行下面的操作！
            {
                //(2)如果找到了操作符，就必须立马拿到操作符，前面的两个数据!

                int right=st.top();
                st.pop();

                int left=st.top();
                st.pop();

                //(3)找到操作符的前两个数据还没有完，我们还必须知道这个操作符是什么样的操作符!!!

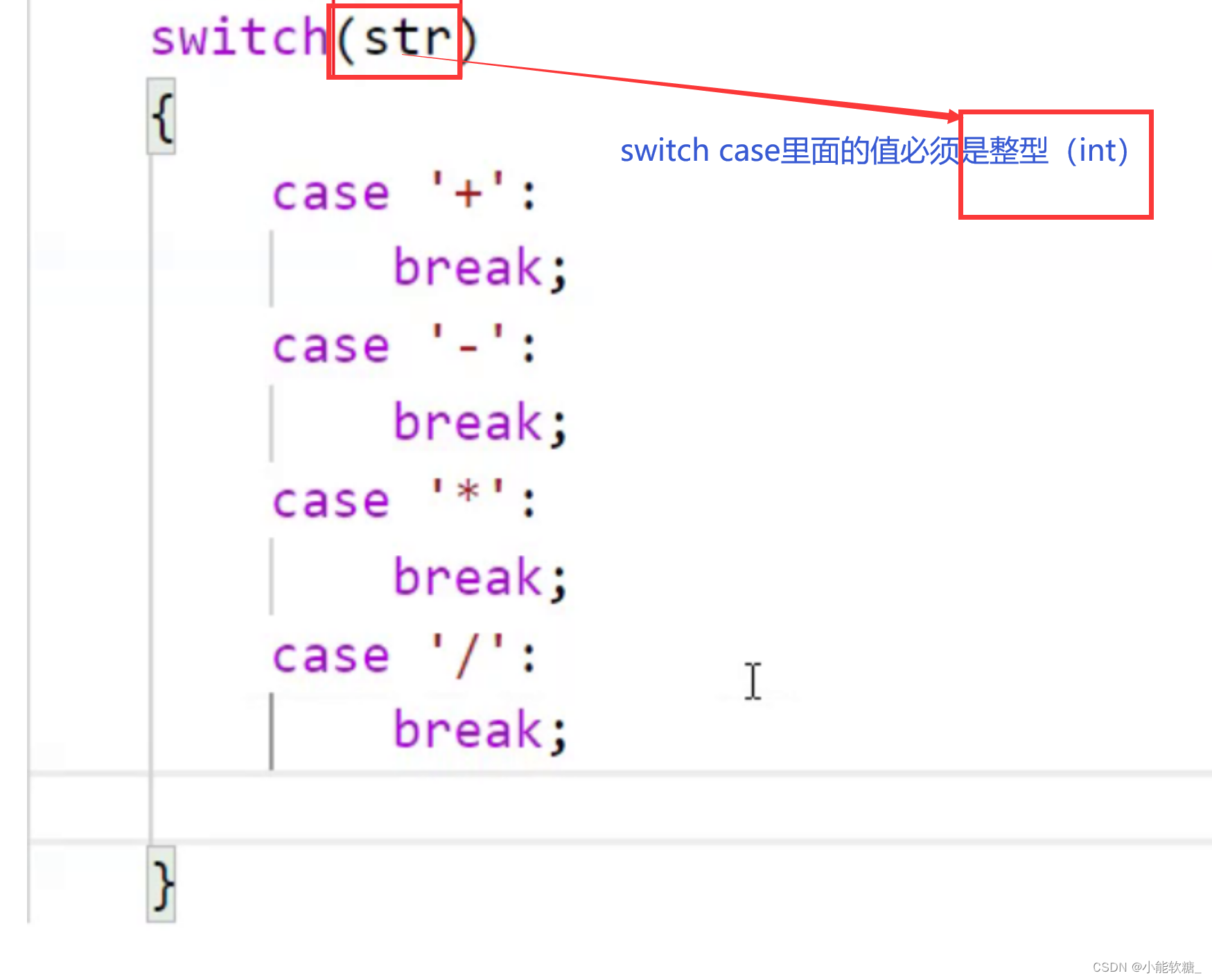
                switch(str[0])
                {
                        //case '+':
                        //st.push(right+left);
                        //break;

                        //case '-':
                        //st.push(right-left);
                        //break;

                        //case '*':
                        //st.push(right*left);
                        //break;

                        //case '/':
                        //st.push(right/left);
                        //break;

                    //两个操作数的执行结果必须是：左(left)在前，右(right)在后！！！只有这样才符合运算逻辑！
                    case '+':
                        st.push(left+right);
                        break;

                        case '-':
                        st.push(left-right);
                        break;

                        case '*':
                        st.push(left*right);
                        break;

                        case '/':
                        st.push(left/right);
                        break;   
                }   
                
            }

            else
            {
                st.push(stoi(str));
            }
        }

        return st.top();
    }
};