MATLAB车辆动力学建模 ——《控制系统现代开发技术》

引言

在上这门课之前，我已经用过CasADi 去做过最优化的相关实践，其中每一步迭代主要就是由：对象系统+优化求解两部分组成的。这里我们重点介绍 “对象系统”如何去描述 ，因为它是每一步迭代中重要的一环——“优化求解”会获得控制输入u，u需要作用于模型，获得状态，以去计算目标函数“代价”。在上该课之前，我并没有系统的认识，因此，这门课让我对自己之前的实践有了全新的认识。

致谢

感谢BIT的智能车辆研究所的于会龙老师，其事无巨细的教导，手把手教学让身为研究牲的我感慨万分。

前言

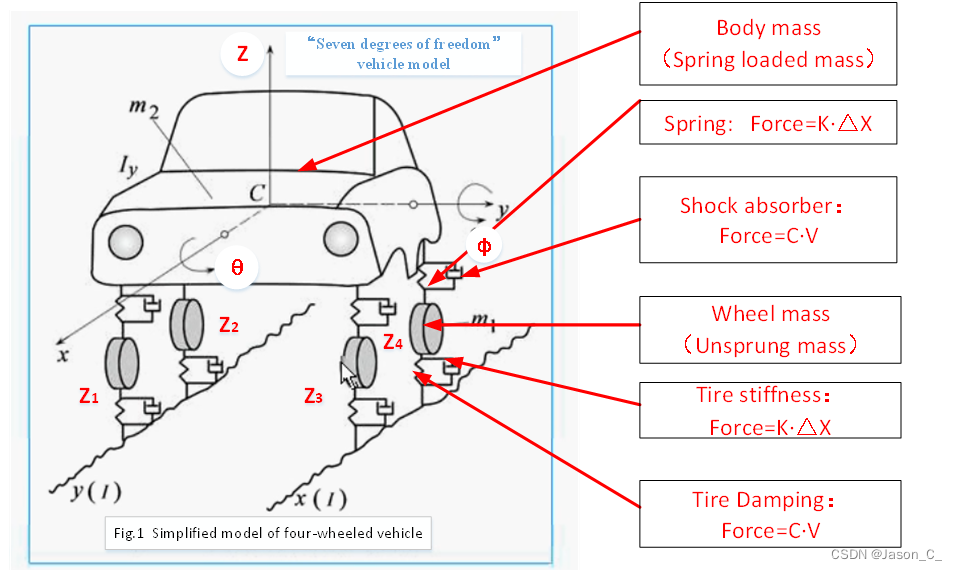
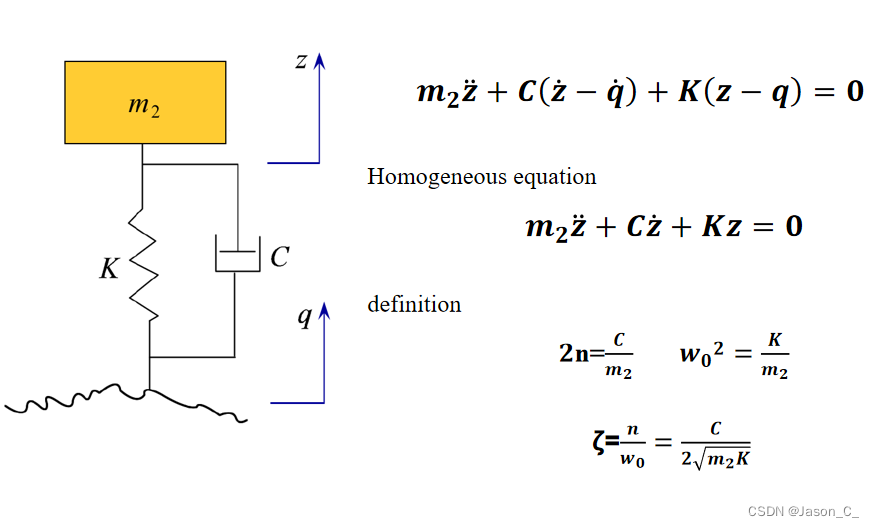
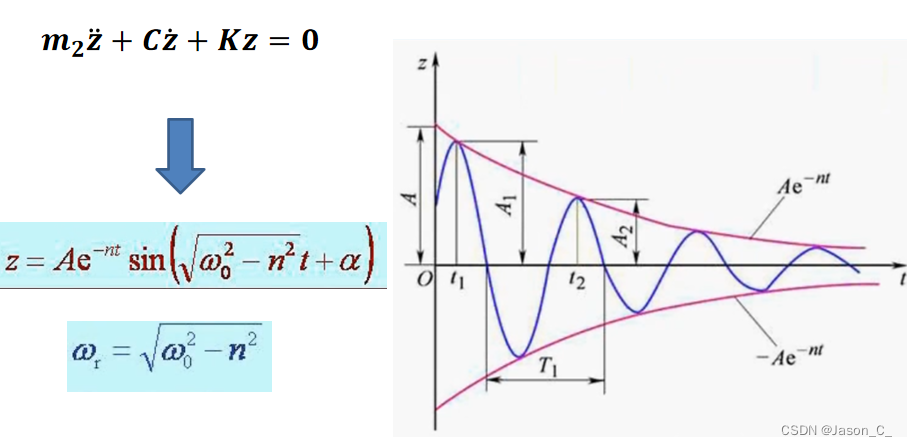
虽然标题是车辆动力学，但例子是车子的垂向减震系统哈。抱歉
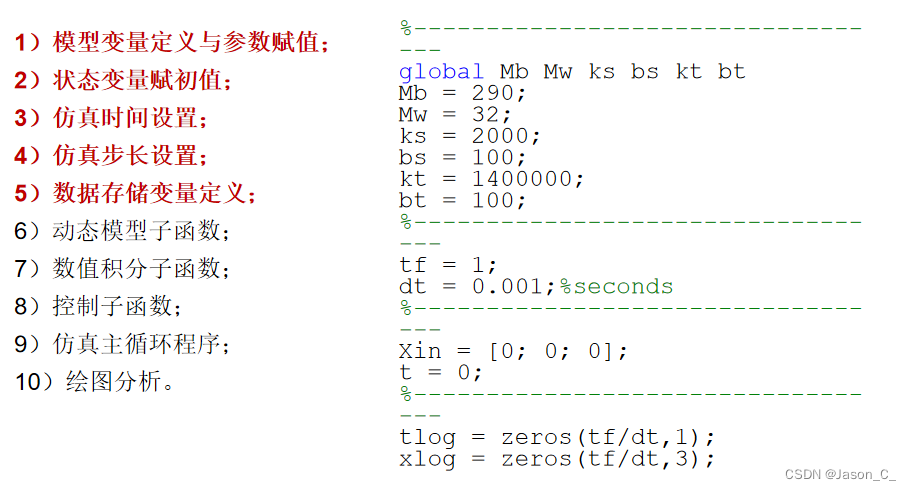
在这里插入图片描述

代码流程

这个流程很重要，大家仔细体会。6)-10)步就不放图了，大家直接在后面的代码里寻找对应的部分。
在这里插入图片描述

数值积分函数

这里提供了三个选择，matlab中给了4阶龙格库塔和欧拉，大家自行选择
在这里插入图片描述

MATLAB代码

clc
clear
clear all
%----------------------------------
global Mb Mw ks bs kt bt
Mb = 290;
Mw = 32;
ks = 20000;
bs = 500;
kt = 1400000;
bt = 100;
%----------------------------------
tf = 1;
dt = 0.001;%seconds
%----------------------------------
Xin = [0; 0; 0];
t = 0;
%----------------------------------
tlog = zeros(tf/dt,1);
xlog = zeros(tf/dt,3);

for i = 1: tf/dt
    u         = -0.1 + 0.2*rand;  %控制子程序  
    Xout      = Euler(@vdn1,Xin,u,t,dt); %积分函数 
    tlog(i)   = t;     %数据存储
    t         = i*dt;  %时间更新
    Xin       = Xout;  %状态更新
    xlog(i,:) = Xin';  %数据存储
end

figure
subplot(3,1,1)
plot(tlog,xlog(:,1),'k');
ylabel('$z_b \,(m) $');
xlabel('$$ t \, (s) $$');
subplot(3,1,2)
plot(tlog,xlog(:,2),'r');
ylabel('$ {\dot z_b} \,(m) $');
xlabel('$$ t \, (s) $$');
subplot(3,1,3)
plot(tlog,xlog(:,3),'b');
ylabel('$ {z_r} \,(m) $');
xlabel('$$ t \, (s) $$');


function dXin = vdn1(t,Xin,u)
global Mb ks bs
%% 状态变量 
Zb   = Xin(1,:); %车身垂向位移
dZb  = Xin(2,:); %车身垂向速度
Zr   = Xin(3,:); %路面接触点垂向位移
%% 求状态变量一阶导数 
dZr  = u(1,:);   %路面接触点垂向位移变化率
ddZb = (-bs.*(dZb-dZr)-ks.*(Zb-Zr))/Mb; %车身垂向加速度%% 状态变量一阶导数
dXin = [dZb;ddZb;dZr];
end

function [y]=runge_kutta4(ufunc,Xin,u,t,h)% ode45
%-----------------------------------------------------------------------------------%
% Author: HUILONG YU, hlyubit@gmail.com.
% Date  : 09/11/2016
% Copyright (C) 2016 HUILONG YU. All Rights Reserved.
%-----------------------------------------------------------------------------------%
k1=ufunc(t,Xin,u);
k2=ufunc(t+h/2,Xin+h*k1/2,u);
k3=ufunc(t+h/2,Xin+h*k2/2,u);
k4=ufunc(t+h,Xin+h*k3,u);

y=Xin+h*(k1+2*k2+2*k3+k4)/6; 
end

function y = Euler(ufunc,Xin,u,t,h)
 
y= Xin+ h * ufunc(t,Xin,u);
end

补充

1、参数中有两个关键参数，决定悬架的“硬度”，【调整悬架参数可抑制路面不平度激励带来的车身振动】
ks = 20000; bs = 500;比 ks = 2000000; bs = 100000; 更好
2、程序每次运行结果不同是因为输入u 里有一个rand随机数。

Python

环境：Windows ，官网安装的python（安装过程中选择将python添加到全局路径），在vscode里直接执行。还需要cmd调出终端安装两个py的模块。

pip install numpy matplotlib

import numpy as np
import matplotlib.pyplot as plt

# 全局变量
Mb = 290
Mw = 32
ks = 20000
bs = 500
kt = 1400000
bt = 100

# 时间设置
tf = 1
dt = 0.001  # 秒

# 初始条件
Xin = np.array([0, 0, 0])
t = 0

# 数据存储
tlog = np.zeros(int(tf/dt))
xlog = np.zeros((int(tf/dt), 3))

# 定义 vdn1 函数
def vdn1(t, Xin, u):
    Zb = Xin[0]  # 车身垂向位移
    dZb = Xin[1]  # 车身垂向速度
    Zr = Xin[2]  # 路面接触点垂向位移
    
    dZr = u  # 路面接触点垂向位移变化率
    ddZb = (-bs * (dZb - dZr) - ks * (Zb - Zr)) / Mb  # 车身垂向加速度
    
    return np.array([dZb, ddZb, dZr])

# 定义 Euler 函数
def Euler(ufunc, Xin, u, t, h):
    return Xin + h * ufunc(t, Xin, u)

# 主循环
for i in range(int(tf/dt)):
    u = -0.1 + 0.2 * np.random.rand()  # 控制子程序
    Xout = Euler(vdn1, Xin, u, t, dt)  # 积分函数
    tlog[i] = t  # 数据存储
    t = (i + 1) * dt  # 时间更新
    Xin = Xout  # 状态更新
    xlog[i, :] = Xin  # 数据存储

# 绘图
plt.figure()

plt.subplot(3, 1, 1)
plt.plot(tlog, xlog[:, 0], 'k')
plt.ylabel('$z_b \,(m)$')
plt.xlabel('$t \,(s)$')

plt.subplot(3, 1, 2)
plt.plot(tlog, xlog[:, 1], 'r')
plt.ylabel('$\dot{z_b} \,(m/s)$')
plt.xlabel('$t \,(s)$')

plt.subplot(3, 1, 3)
plt.plot(tlog, xlog[:, 2], 'b')
plt.ylabel('$z_r \,(m)$')
plt.xlabel('$t \,(s)$')

plt.tight_layout()
plt.show()