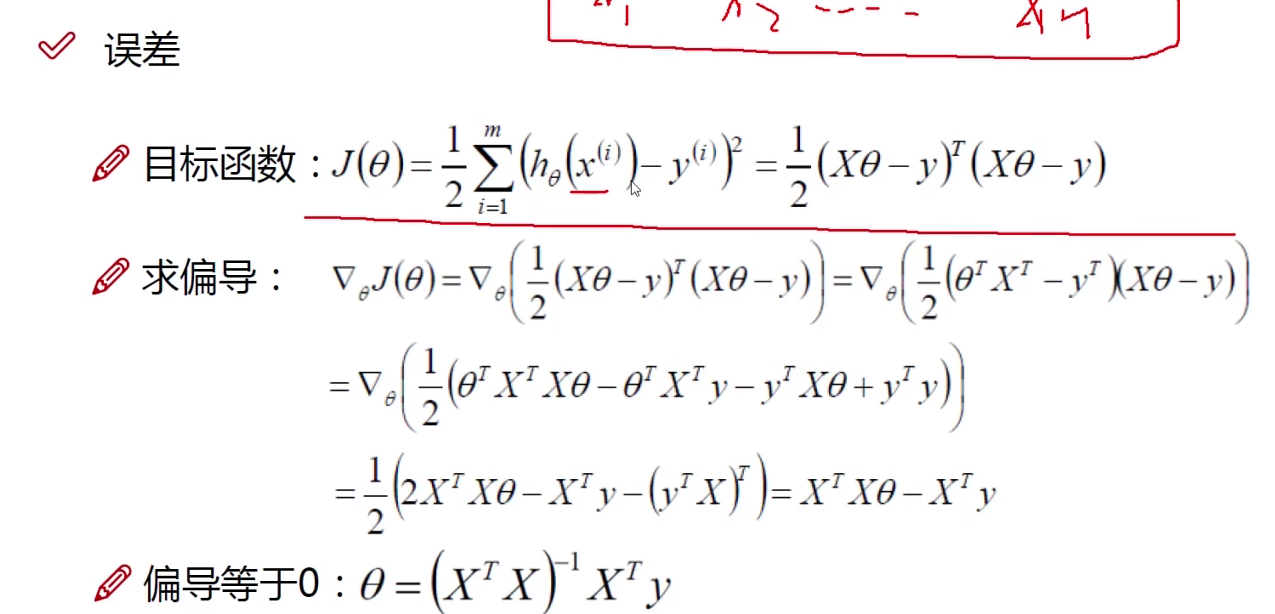线性回归
例子
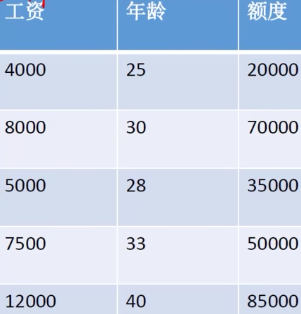
数据:工资和年龄(两个特征)
目标:预测银行会贷款给我们多少钱(标签)
思路:工资和年龄都会影响最终银行带宽的结果,那么它们各自由多大影响呢(参数)
通俗解释
X1、X2就是两个特征(年龄、工资)Y是银行最终会借给我们多少钱
找到最合适的一条线(想象一个高纬)来最好的拟合我们的数据点
假设是年龄的参数,
是工资的参数,
是偏置项
拟合的平面:
新加一列(=1):
整合:
真实值和预测值之间肯定要存在差异(用来表示该误差)
对于每个样本:

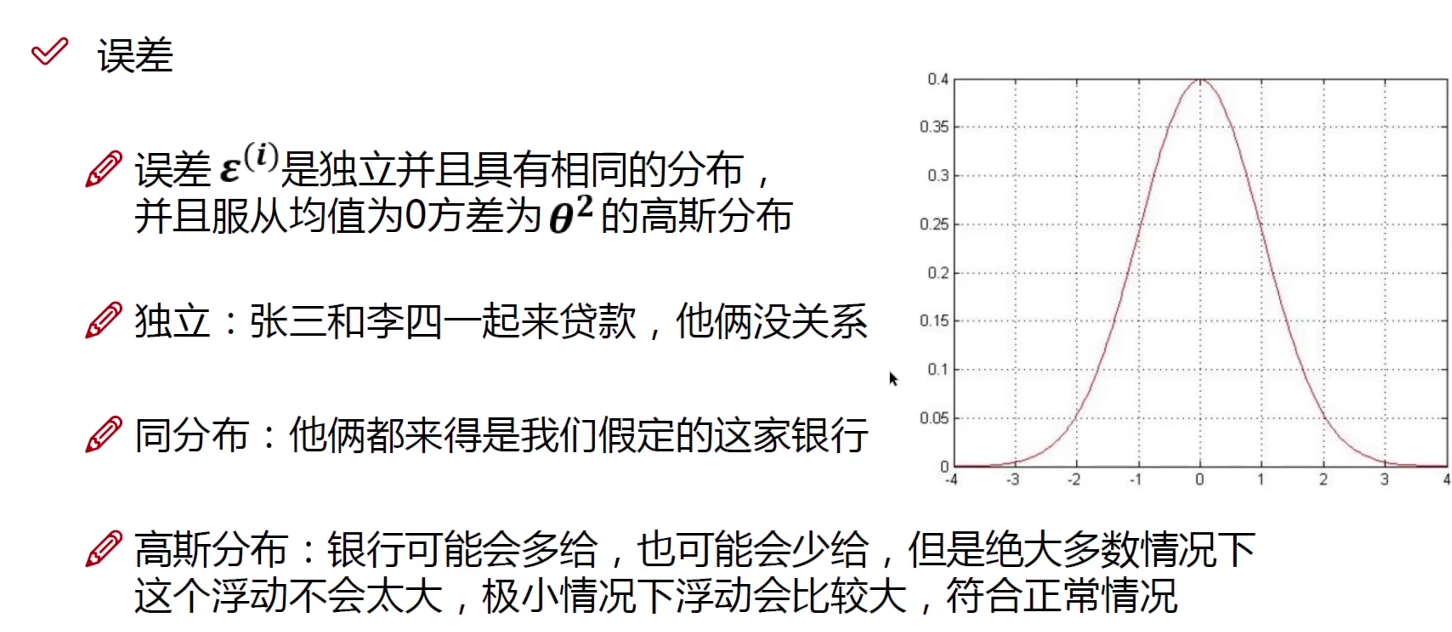
高斯分布
高斯分布,也被称为正态分布(Normal Distribution),是一个在统计学中非常重要的概率分布。
正态分布是一类连续概率分布,其形状呈现为对称的钟形曲线,这种曲线被称为高斯函数或高斯钟形曲线。高斯分布的数学表达式可以表示为:
正态分布有两个参数:均值和方差
,它们决定了分布的形状和位置。均值决定了分布的中心位置,标准差决定了分布的离散程度,即数据集中或分散的程度。标准差越大,分布越宽;标准差越小,分布越窄。
高斯分布在自然科学和社会科学中十分常见,因为许多随机变量的分布都近似是正态分布,特别是当独立随机变量的总和趋于无限时,根据中心极限定理,其分布接近正态分布。
标准正态分布是当正态分布的均值且标准差
时的特殊情况,标准正态分布表达式如下:
标准正态分布是正态分布的一个标准化形式,通常用于简化问题的求解过程,在统计分析中具有重要应用。任何正态分布都可以通过标准化过程(即从每个数据点中减去均值并除以标准差)转换为标准正态分布。这个过程称为标准化或归一化。
总结来说,所有的标准正态分布都是正态分布,但不是所有的正态分布都是标准正态分布。标准正态分布是正态分布中的一个特例。
:意思是在
和
下y的概率
预测值与误差:
由于误差服从高斯分布:
将(1)式带入(2)式:
为什么用累乘